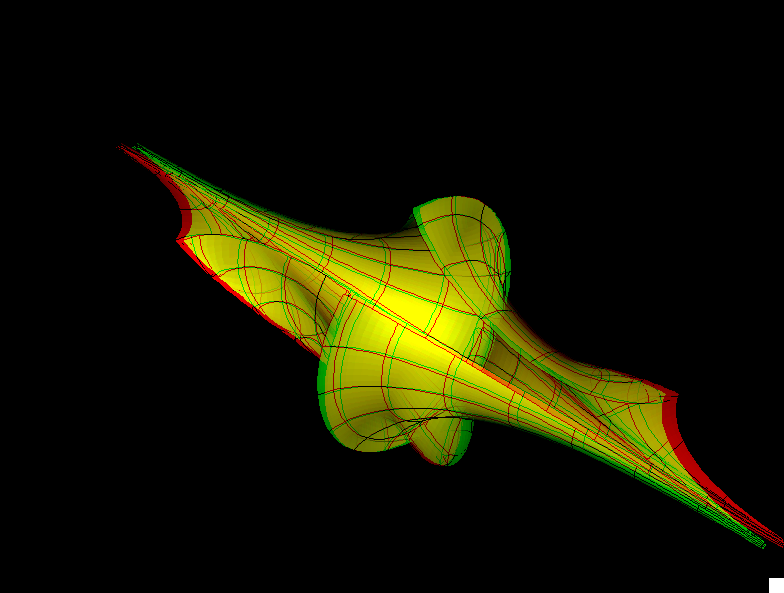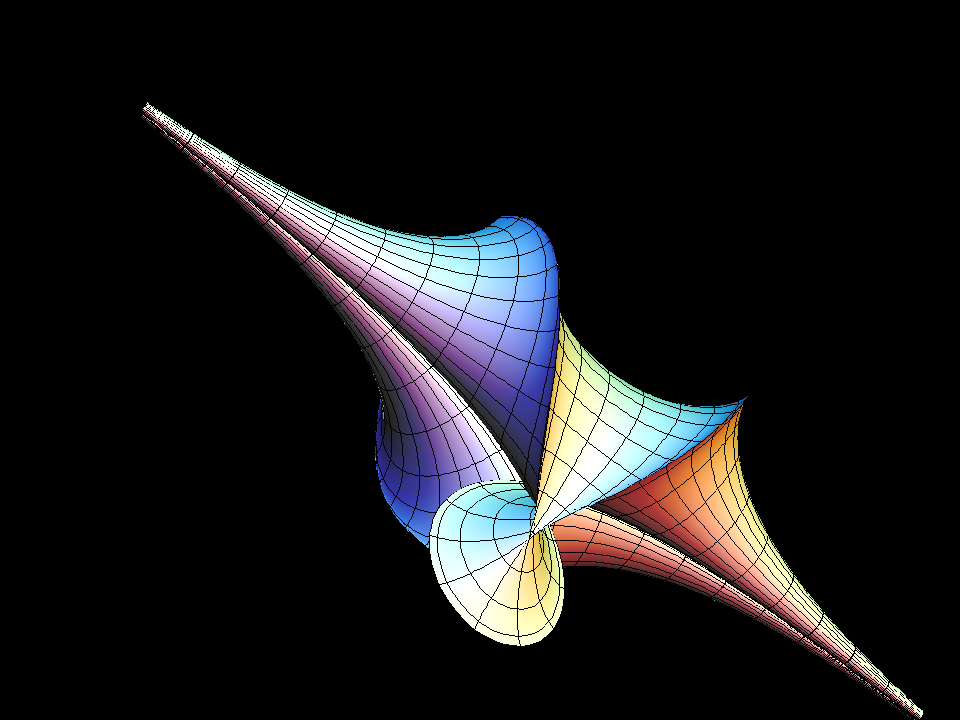

The Two-Soliton Surface surface is the surface of Gaussian curvature K = -1 that corresponds to the following solution of the Sine-Gordon equation:
q(u,v) := 4 * arctan( B * (exp(A2(u, v)) - exp(A1(u, v))) / (1 + exp(A1(u, v) + A2(u, v))));
where:
B := (cos(bb * π) - cos(aa * π)) / (cos((bb - aa) * π) - 1); A1 := cosec(aa * π) * u - cotan(aa * π) * v; A2 := cosec(bb * π) * u - cotan(bb * π) * v;
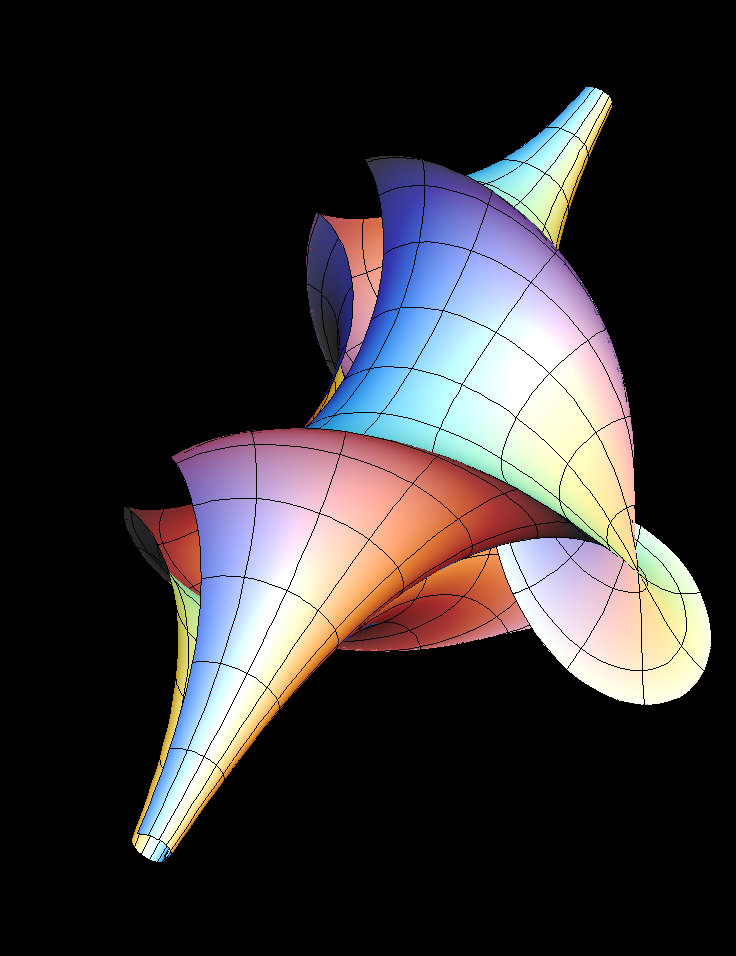
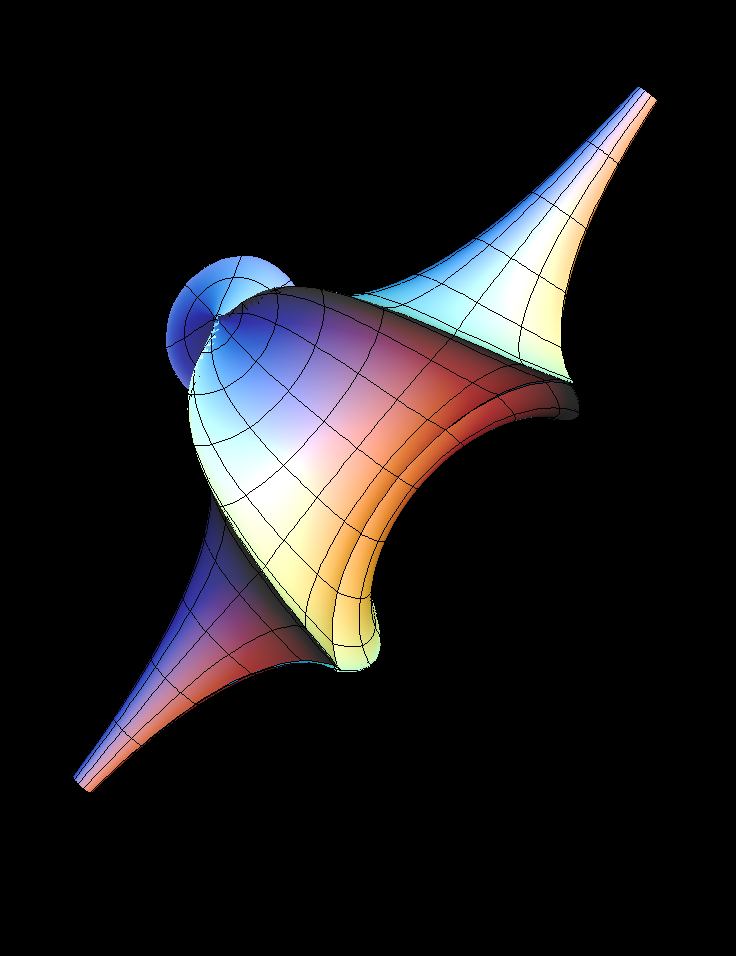

Let us summarize, how the more complicated pseudospherical surfaces
are constructed. If one parametrizes a surface of Gauss curvature K = -1
in special (so called “asymptotic”) coordinates, then the angle
q(x,t)
between the parameter lines determines the so called first and second
fundamental forms of the surface. Once these forms are given, the
surface can be obtained by solving (numerically if necessary) a pair
of ODEs for the parameter lines. The fundamental theorem of surface
theory says: a necessary and sufficient condition for this construction
is, that the two fundamental forms satisfy the Gauss- and Codazzi-
integrability conditions. In the case of our special asymptotic
coordinates these integrability conditions simplify enormously to:
“The angle function q(x,t) must satisfy the Sine-Gordon equation (SGE)”
,
which is:
d/dt d/dx q(x,t) = sin(q(x,t))
A second function
Q(x,t)
is called a “Bäklund transformation with
parameter s” if
Q(x,t)
satisfies a pair of first order equations:
dQ/dx(x,t) = +dq/dx(x,t) + 2 s * sin( (Q+q)(x,t)/2 )dQ/dt(x,t) = -dq/dt(x,t) + 2/s * sin( (Q-q)(x,t)/2 )Q(x,t) can be found from these two ODEs, if
q(x,t)
is an SGE solution
and then Q(x,t) is also an SGE solution.
If one starts with
q(x,t) = 0
then one obtains
Q(x,t) = 4 * arctan(exp(s*x + t/s))
. From
Q(x,t)
the
Dini Surface
are obtained.
An SGE marvel is that any pair s1, s2 of Bäklund parameters (with
SGE solutions
Q1(x,t)
,
Q2(x,t)
allow to explicitly give another
SGE solution
Qq(x,t)
, namely:
tan( (Qq(x,t) - q(x,t))/4 ) = (s1+s2)/(s1-s2)*tan ( (Q1(x,t) - Q2(x,t))/4 )
.
The 2-Soliton solutions are obtained by choosing any real pairs
s = s1
,
s = s2
(with s the parameter in the Bäcklund transformation pairs of ODEs above).
The construction also works with complex parameters
s1 = z, s2 = conj(z)
.
In this case Q1 and Q2 are not real functions, but Qq turns out to be real
again. If
|z| = 1
, one gets the surfaces called “breathers” and for other z
one gets deformations of breathers like the image above.