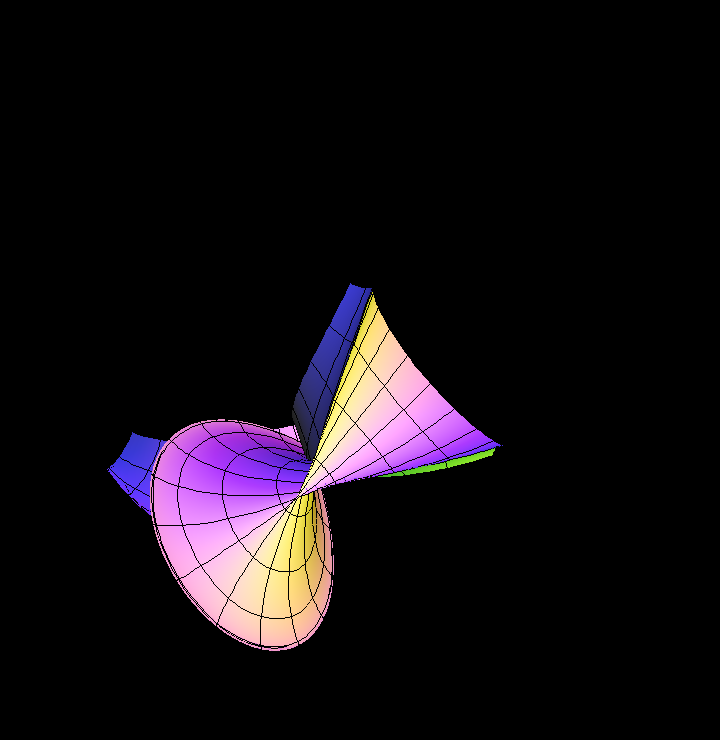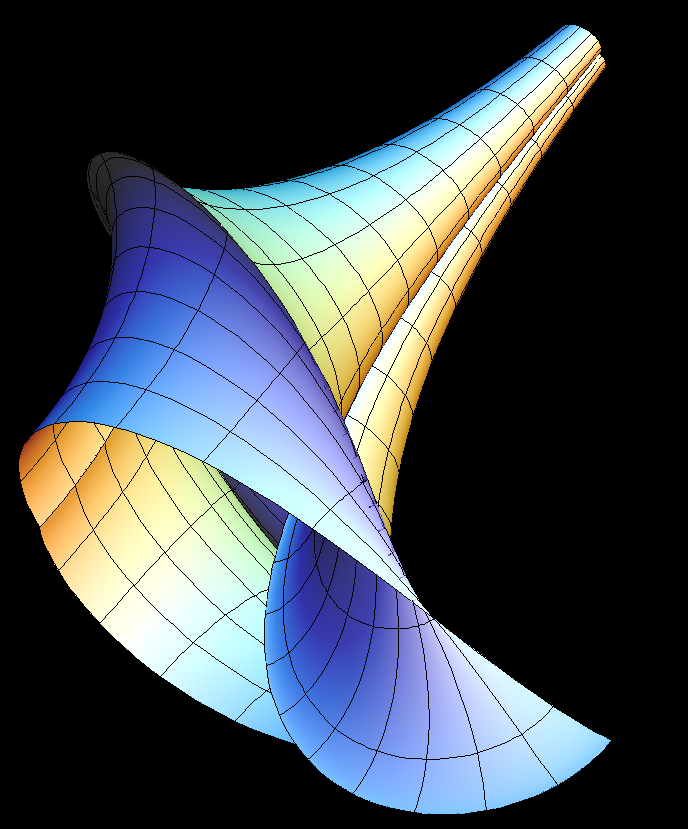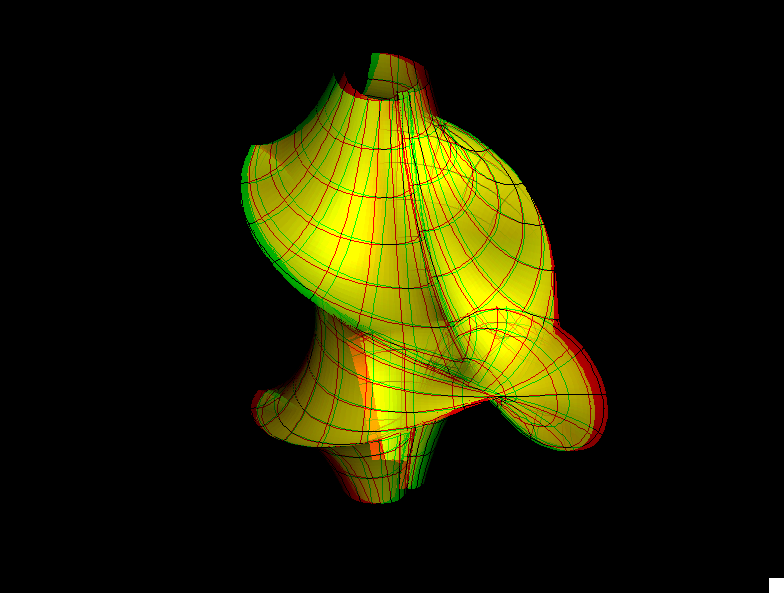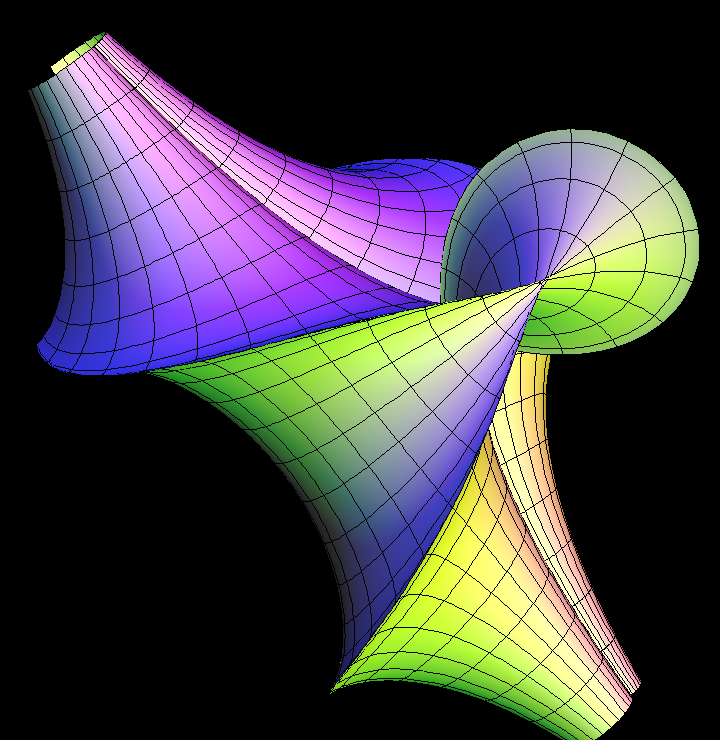

This surface of constant Gaussian curvature K = -1 was discovered early. It is very popular because of its beauty.
Kuen Surface Parametric Equations x = 2 * cosh(v) * (cos(u) + u * sin(u)) / (cosh(v) * cosh(v) + u * u) y = 2 * cosh(v) * (-u * cos(u) + sin(u)) / (cosh(v) * cosh(v) + u * u) z = v - (2 * sinh(v) * cosh(v)) / (cosh(v) * cosh(v) + u * u)
Note that K = -1 surfaces necessarily have the sharp singular rims.
There is a famous theorem by Hilbert which says: The complete hyperbolic plane (i.e. the plane with a complete metric that has Gaussian curvature K = -1) cannot be isometrically (i.e. arc length preserving) immersed (i.e. mapped so that the derivative has no singularities) into Euclidean R^3. The proof has a surprisingly constructive aspect: You pick any regular point of a (K = -1)-surface in R^3. Then you can compute a distance D such that within distance D from the chosen point the pair of asymptote lines (i.e. curves on the surface with normal curvature = 0) becomes tangential to each other. The points where the asymptote lines touch ( instead of intersect) each other are those sharp singular rims.