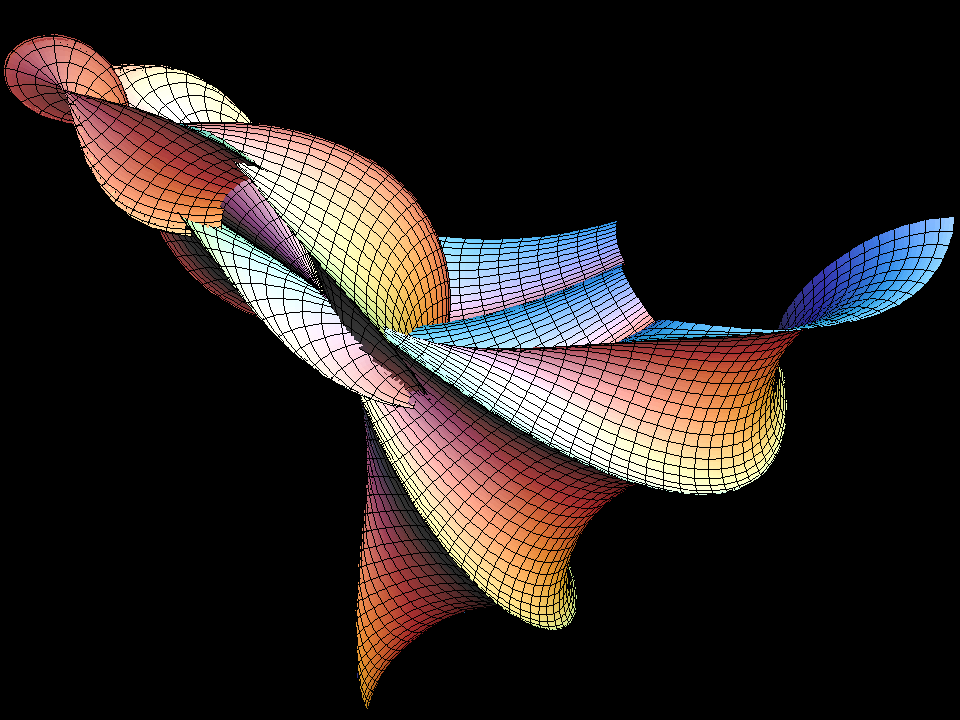
(K = -1)
surface made from a 4-soliton SGE solution. The 4-soliton q(u,v) depends on four real constants a,b,c,d.
The Bianchi-Bäcklund transform leads to more and more complicated, but
explicit, solutions q(u,v) of the Sine-Gordon Equation (SGE). Each SGE
solution determines a parametrized surface F(u,v) with Gauss curvature
K = -1
.
In spite of the sharp rims these surfaces are defined for all (u,v)
in R^2. The singular rims occur in a similar way as the cusps of rolling
curves: At the zeros of sin(q(u,v)) the velocity of one set
of parameter lines becomes zero and the parameter lines reverse their direction,
so that each produces a cusp and all these cusps are a rim.
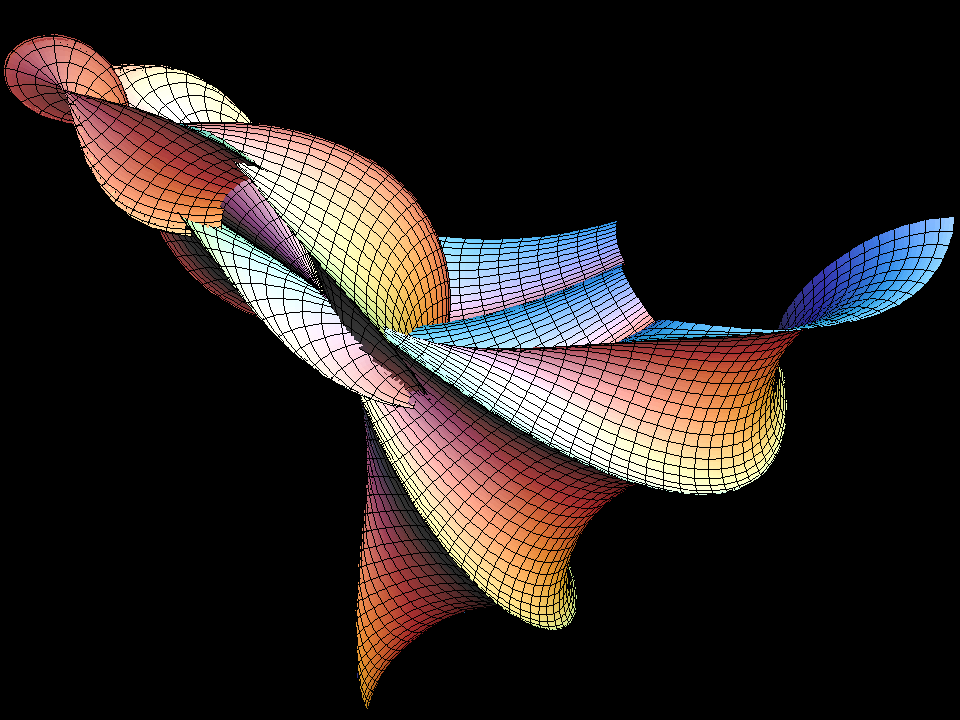
(K = -1)
surface made from a 4-soliton SGE solution. The 4-soliton q(u,v) depends on four real constants a,b,c,d.
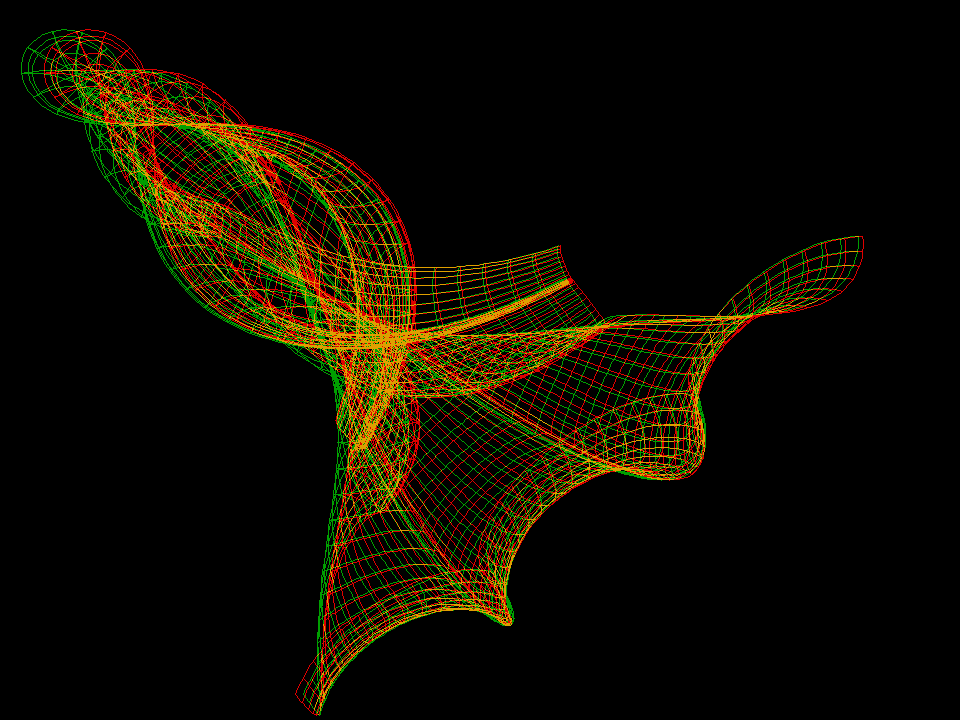
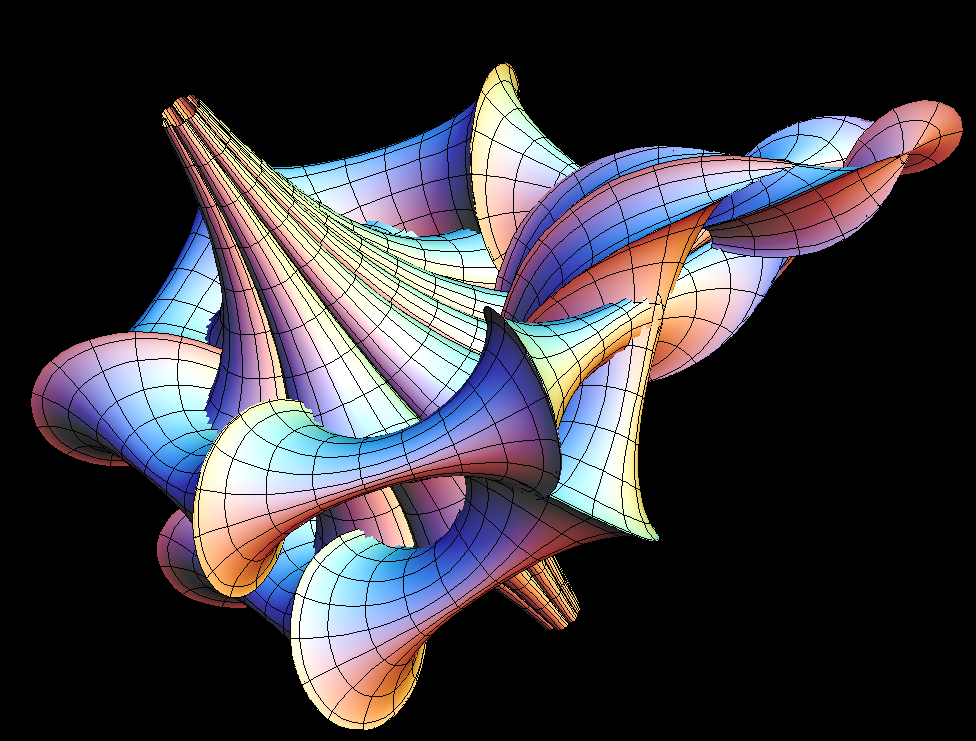
(K = -1) surface made from a 4-soliton SGE solution. The
4-soliton q(u,v) depends on two complex constants
z=a+i*b
,
w=c+i*d
,
but still is a real SGE solution.
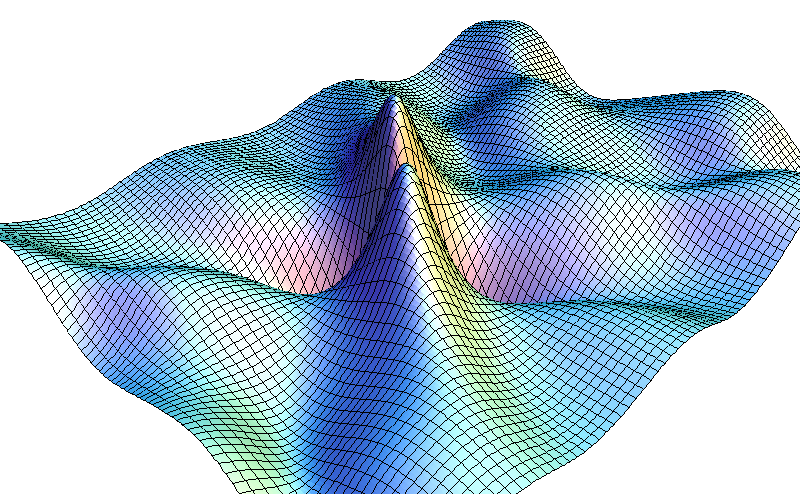
q(u,v) of the previous surface is shown as the graph
(u,v,q(u,v))
.
This solution is called double breather.