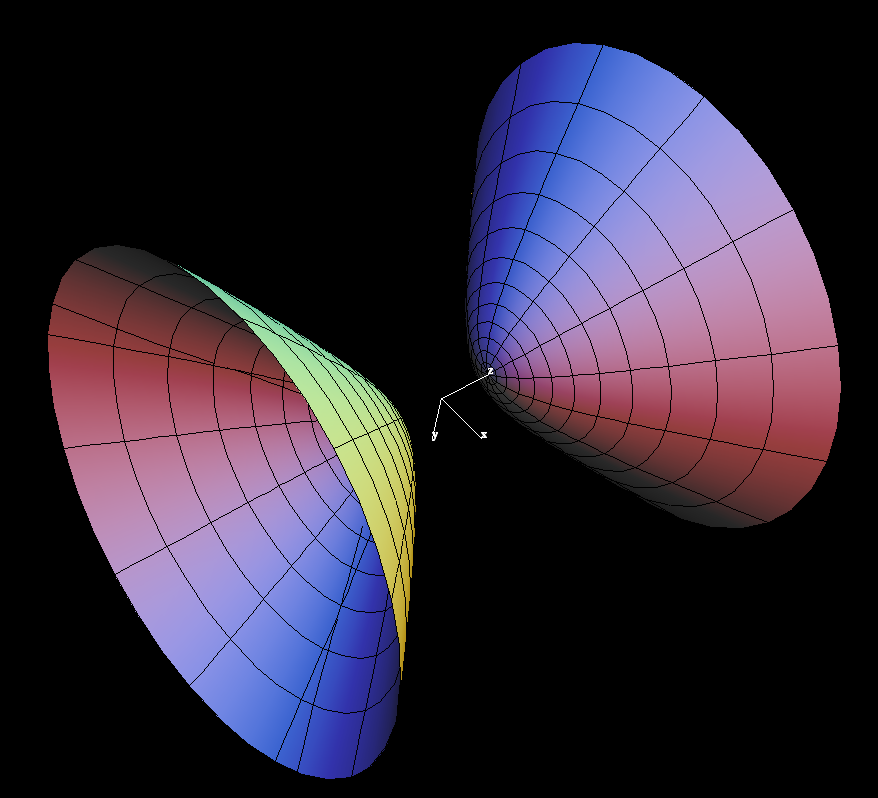
(u, φ) ⟶ (sinh(u)*cos(φ), sinh(u)*sin(φ), ± cosh(u) )
The analogy of the 2-sheeted hyperboloid with the Euclidean unit sphere
becomes apparent, if one sees it as the time unit sphere in Special Relativity.
For visualization reasons we use only 2 space dimensions, that is, we use
R^3 together with the Lorentz norm
x^2 + y^2 - z^2
.
Vectors for which the Lorentz norm is positive, are called “spacelike”, if vectors have negative Lorentz norm they are called “timelike”, and in case of zero Lorentz norm the name is “lightlike”.
The time unit sphere is the solution set of
x^2 + y^2 - z^2 = -1
.

(u, φ) ⟶ (sinh(u)*cos(φ), sinh(u)*sin(φ), ± cosh(u) )
The meridians (or longitudes), φ = const, are:
u ⟶ (sinh(u)*cos(φ), sinh(u)*sin(φ), ± cosh(u) )
they have the tangent vectors:
(x,y,z) = (cosh(u)*cos(φ), cosh(u)*sin(φ), ± sinh(u) )
with Lorentz norm
x^2 + y^2 - z^2 = +1
. This means, the meridians are
spacelike and parametrized by arc length.
The latitudes, u = const, are:
φ ⟶ (sinh(u)*cos(φ), sinh(u)*sin(φ), ± cosh(u) )
.
They are circles in planes parallel to the x-y-plane with (Euclidean)
radius sinh(u) and therefore
circumference = 2*π*sinh(u)
.
Since the meridian-radius, because of the arclength parametrization, has only length = u, we have: The geometry of the time unit sphere has the spectacular property:
circles of radius = u have the circumference = sinh(u)
.
One says: The Riemannian metric of this geometry is
ds^2 = du^2 + sinh(u)^2*d φ^2
This implies: Such a circle has area
2*π*(cosh(u) - 1)
.
In short: length and area of circles grow exponentially with the radius. Differential geometers derive from this behavior of circles that the Gaussian curvature of the time unit sphere is constant = -1.

Remember: the hyperbolic arclength of the meridians is much shorter than the Euclidean interpretation suggests, while the hyperbolic length of the latitude circles is in agreement with our Euclidean eyes. The circumference really grows exponentially as a function of the radius.
The next analogy with the Euclidean sphere is: There are many linear Lorentz isometries which map the hyperboloid to itsself:
(x,y,z) ⟶ cosh(u)*x + sinh(u)*z, y, sinh(u)*x + cosh(u)* z)
Clearly, if
x^2 + y^2 - z^2 = -1
, then the Lorentz norm of the
image is also -1.
The rotations around the z-axis:
(x,y,z) ⟶ (cos(φ)*x - sin(φ)*y, sin(φ*)x + cos(φ)*y, z)
also leave the Lorentz norm invariant. These two families of maps are enough, to map (0, 0, 1) to any other point of the positive sheet of the hyperboloid.
And we can exchange the two sheets:
(x,y,z) ⟶ (coshu)*x + sinh(u)*z, y, -(sinh(u)*x + cosh(u)* z))
Note that these maps are like reflections: applying them twice gives the identity. Also, (0,0,-1) can be mapped to any point on the positive sheet with one of these reflections plus a rotation.


The simple form of the metric implies that any curve from (0, 0, 1) to a point on the latitude circle of hyperbolic radius u has at least the length u. This implies, that the meridians are shortest connections between any two of its points. We therefore view the meridians as straight lines of our hyperbolic geometry. Note that they lie in planes through the origin, which is the midpoint of the hyperboloid. Our linear Lorentz isometries leave the origin fixed and map planes to planes. Since they also map shortest connections between points to shortest connections between the image points, we have another analogy to the Euclidean sphere: Shortest connections (or "straight lines" of the geometry) lie in planes through the origin.
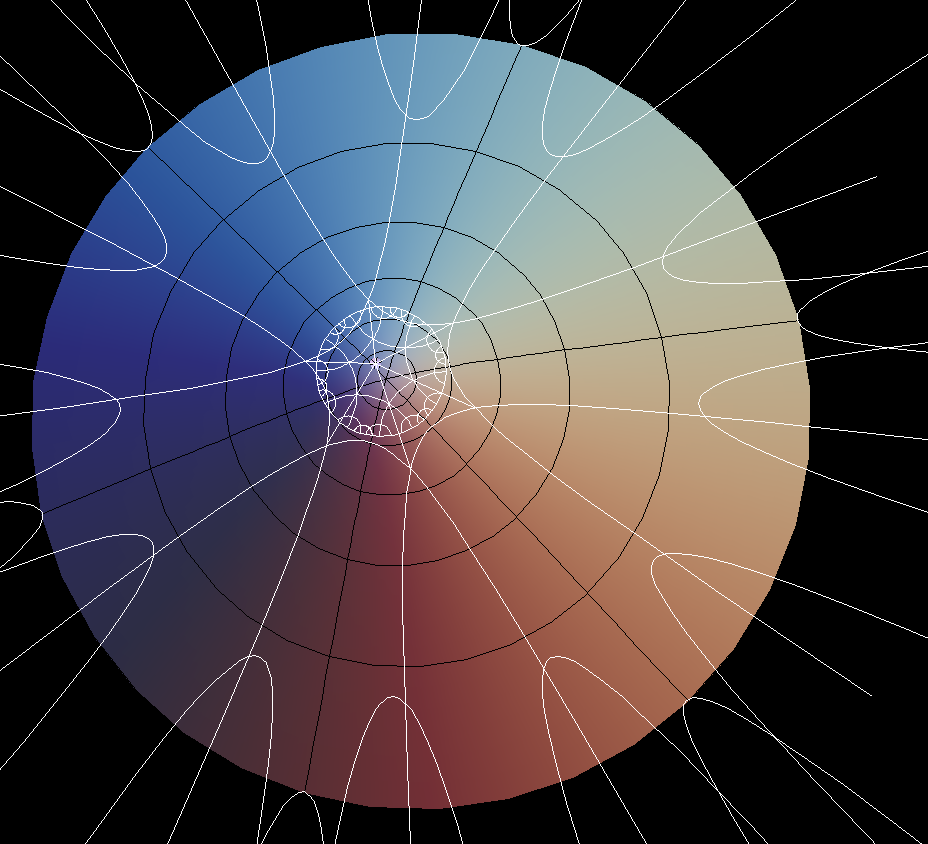
Now that we have straight lines, we can do triangle geometry. All
Euclidean triangle formulas have simple hyperbolic analogues.
For example the Pythagorean theorem for triangles with edge lengths
a,b,c and angle π/2 opposite c reads:
cosh(c) = cosh(a)*cosh(b)
.
For very small triangles this is almost the Euclidean formula,
since
cosh(x) = 1 + x^2/2 + higher order terms
.
One important result is: The angles of a hyperbolic triangle with edge lengths a,b,c are smaller than the angles of a Euclidean triangle with the same edgelengths. And there are intriguing formulas: The area of a triangle with angles α, β, γ is:
area = π - (α + β + γ)
.
One can use triangles to make regular polygons and tesselate the
hyperbolic plane in many different ways. For examples there are
equilateral triangles with all three angles = π/n for any
n ≻ 3
and squares with all four angles = π/n for n ≻ 2
.
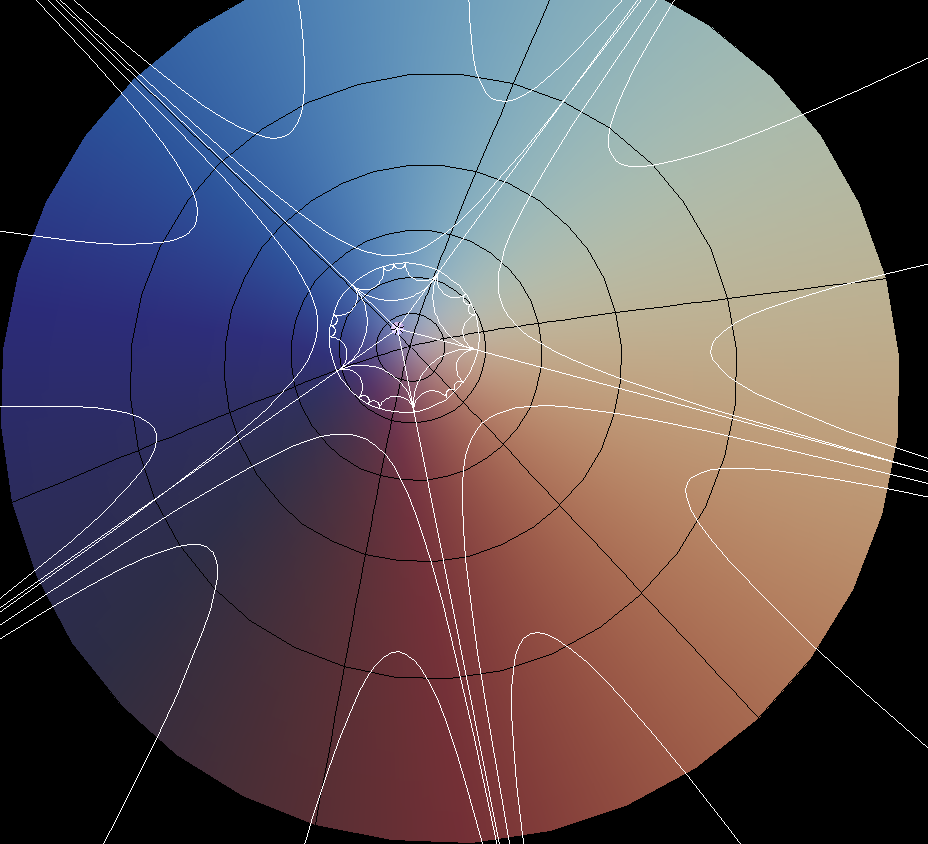
Regular hyperbolic polygons exist with arbitrarily small angles. Even the angle zero is possible - the vertices are then at infinity and the straight lines to the same infinite vertex are called “asymptotic”. The picture shows pentagons with zero degree angles, on the hyperboloid and projected to the x-y-plane.

An anaglyph image of the previous situation. The projection rays lie on a cone which is asymptotic to the hyperboloid.
Stereographic projection is a very important conformal map from the Euclidean sphere to the plane. Similarly we can project the positive sheet from (0,0,-1) to the x-y-plane (which is parallel to the tangent plane at (0,0,1), opposite to the projection center).
We get as image the unit disk in the x-y-plane. We prove that this map is angle preserving (= conformal):
Any two lines (in the x-y-plane) that intersect at p inside the unit disk, represent an angle at p.
The two planes through these lines and the projection center intersect the tangent plane (at (0,0,-1)) with parallel lines, i.e. with a congruent angle. The image of p in the positive sheet and (0,0,-1) can be interchanged by one of the hyperbolic reflections discussed above. This reflection maps the planes into themselves and therefore the angle at (0,0,-1) to the angle at the image point of p. This proves that this projection is conformal. Therefore the image disk is taken as the most important model of hyperbolic geometry, namely the disk model of complex analysis. The “Straight lines” of hyperbolic geometry are, in this model, circles which intersect the unit circle orthogonally.