

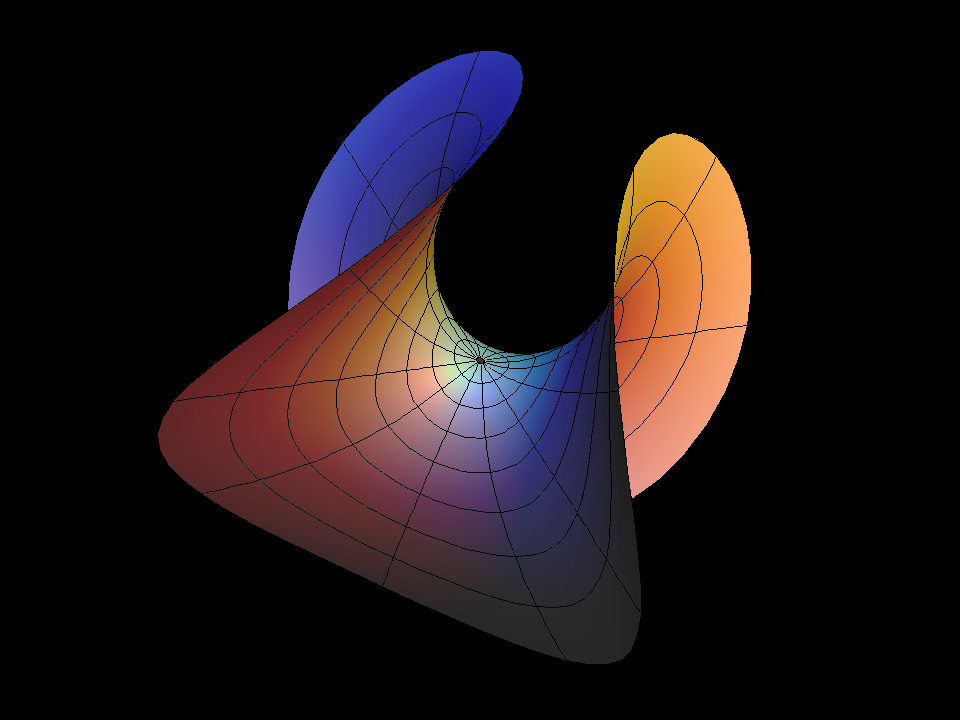
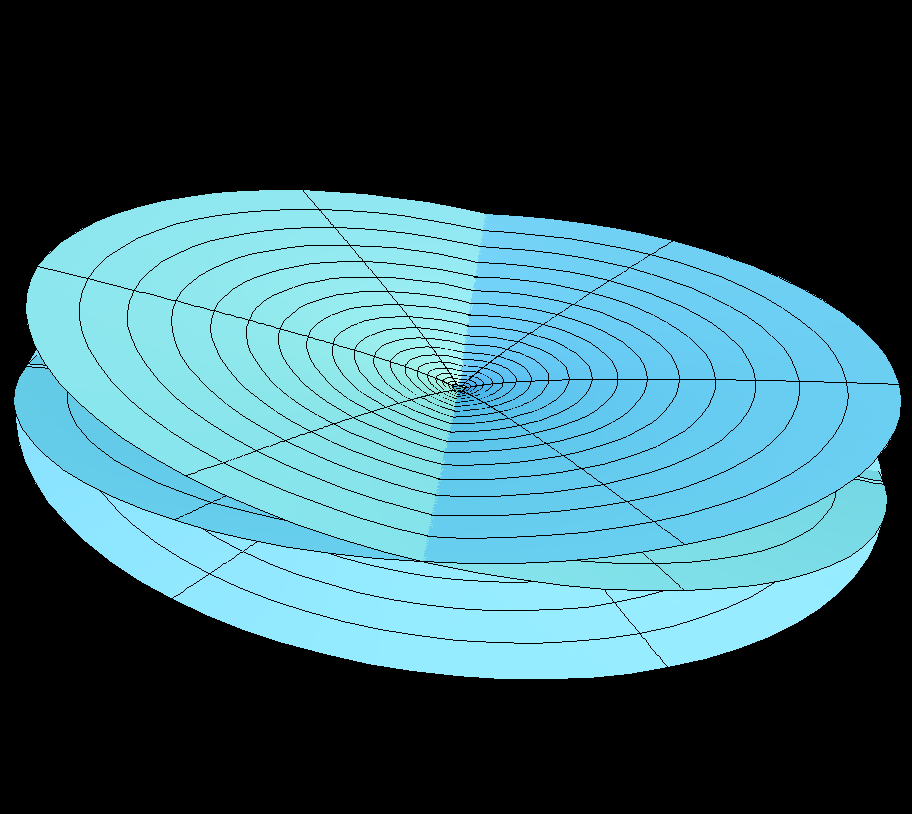
Here's how to visualize Enneper Surface looks like from far away.

x(t) = R * cos(3t), y(t) = R * sin(3t), z(t) = 0, t goes from 0 to 2 π, R is radius of earth.
Then “lift” it so that you have two maxima and 2 minima of z(t):
x(t) = R * cos(3t), y(t) = R * sin(3t), z(t) = h * cos(2t)
(h much smaller than R).
Connect each point of this path to center of the earth. This surface is what Enneper looks like from far away.
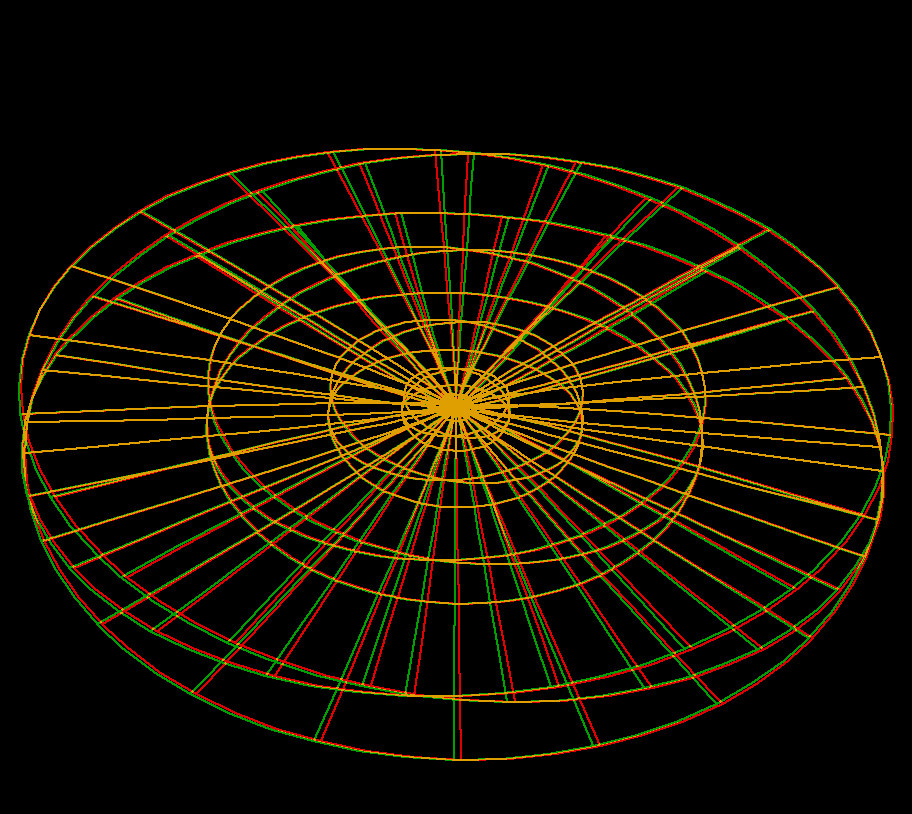
Generalizations to Ennerper with higher symmetry were found 100 years later.
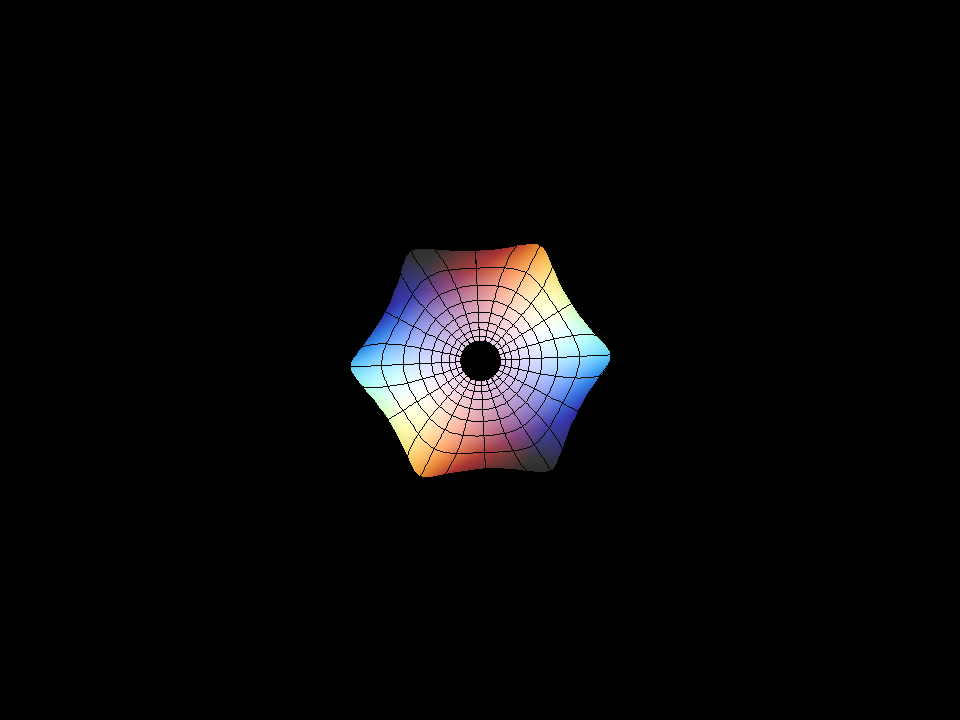
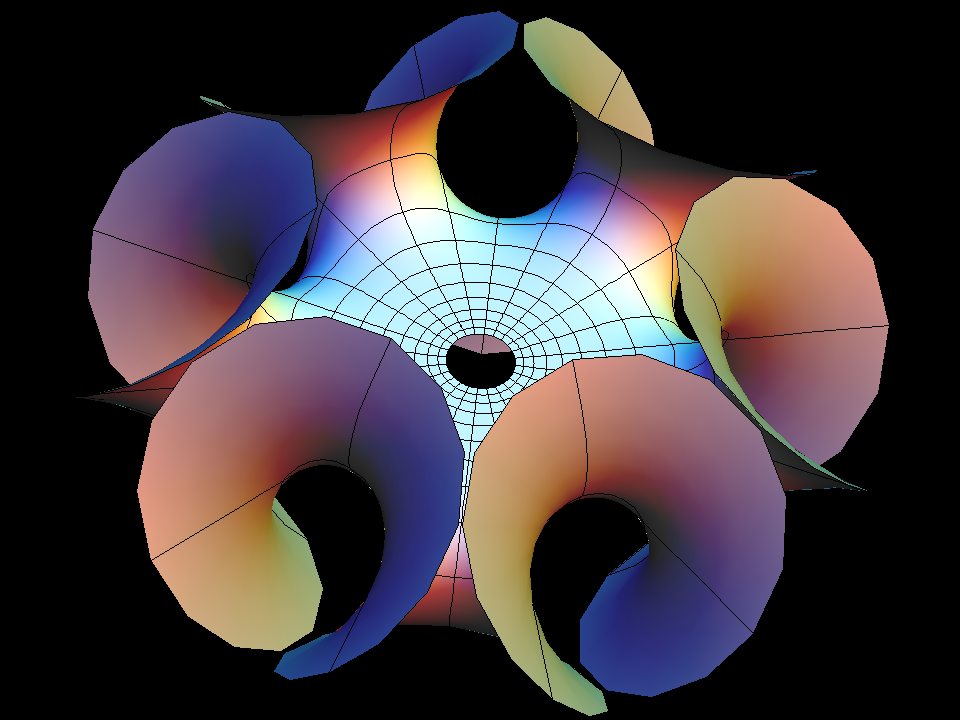
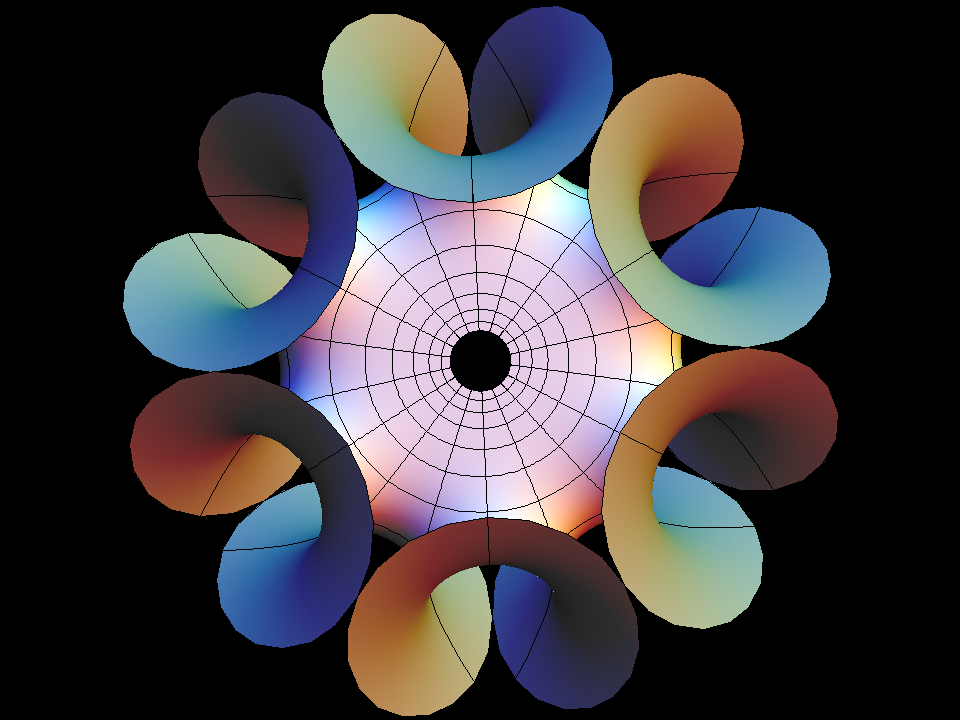
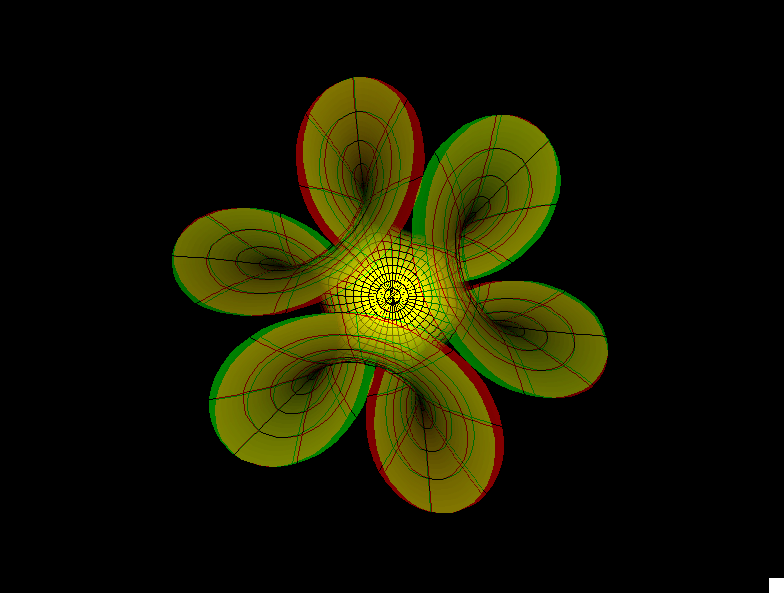

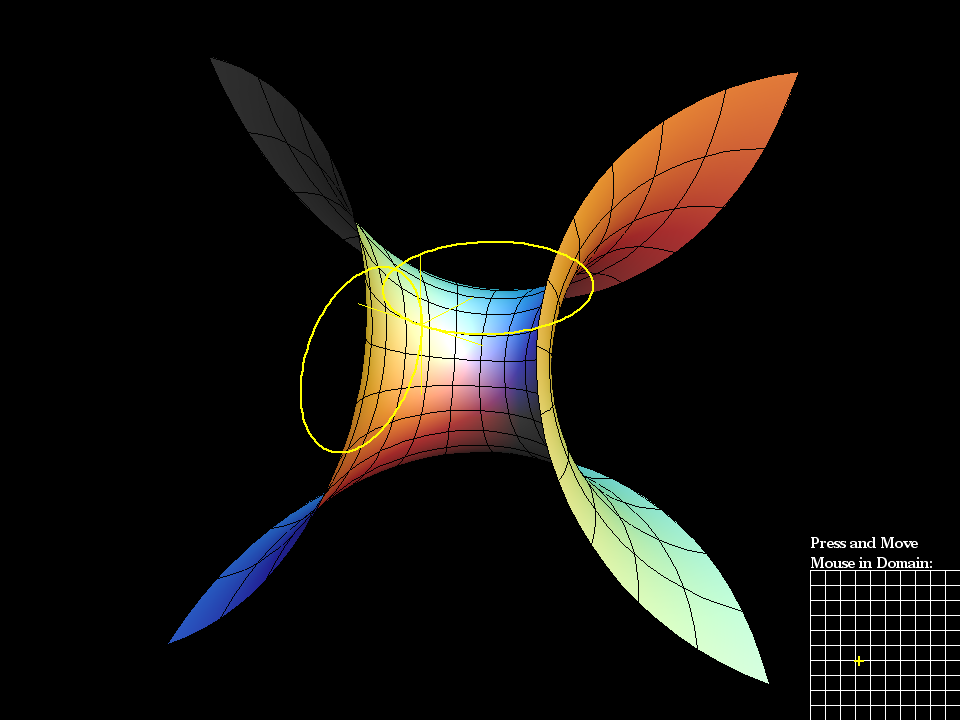
Enneper Surface Parametric Equations
x = u - u * u * u / 3 + u * v * v y = v - v * v * v / 3 + v * u * u z = u * u - v * v
Enneper Surface is one of the finite total curvature immersions discovered in the 19th century. The generalizations to higher symmetry came in the 1980th.
The surfaces Wavy Enneper, Catenoid Enneper, Planar Enneper, and Double Enneper are finite total curvature minimal immersions of the once or twice punctured sphere — shown with standard polar coordinates. These surfaces illustrate how the different types of ends can be combined in a simple way.
The pure Enneper surfaces (Gauss(z)=z^k, k=ee+1) and the Planar Enneper have been re-discovered many times, because the members of the associate family are CONGRUENT surfaces (as can be seen in an associate family morphing) and the Weierstrass integrals integrate to polynomial (respectively) rational immersions.
Double Enneper was one of the early examples in which I joined two classical surfaces by a handle.
Formulas are taken from:
For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see: