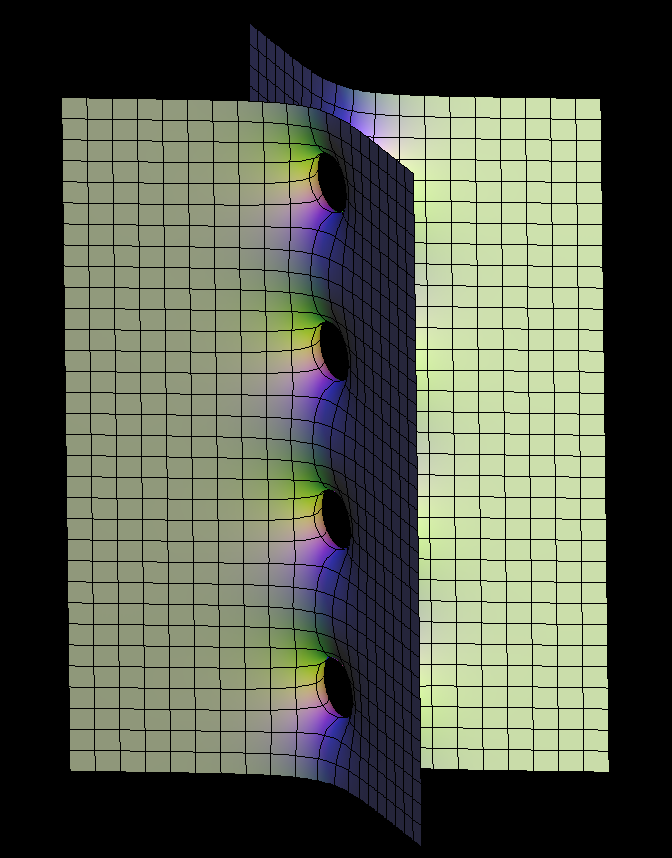

Saddle Tower is Scherk's singly periodic minimal surface generalized to a family, by Hermann Karcher in 1988.
[see Scherk Surface]
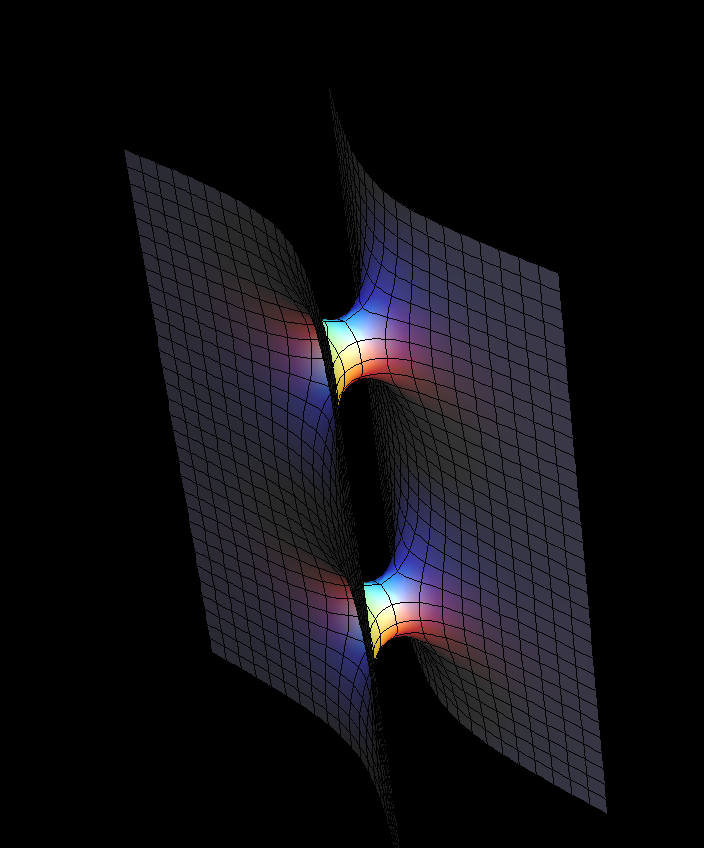
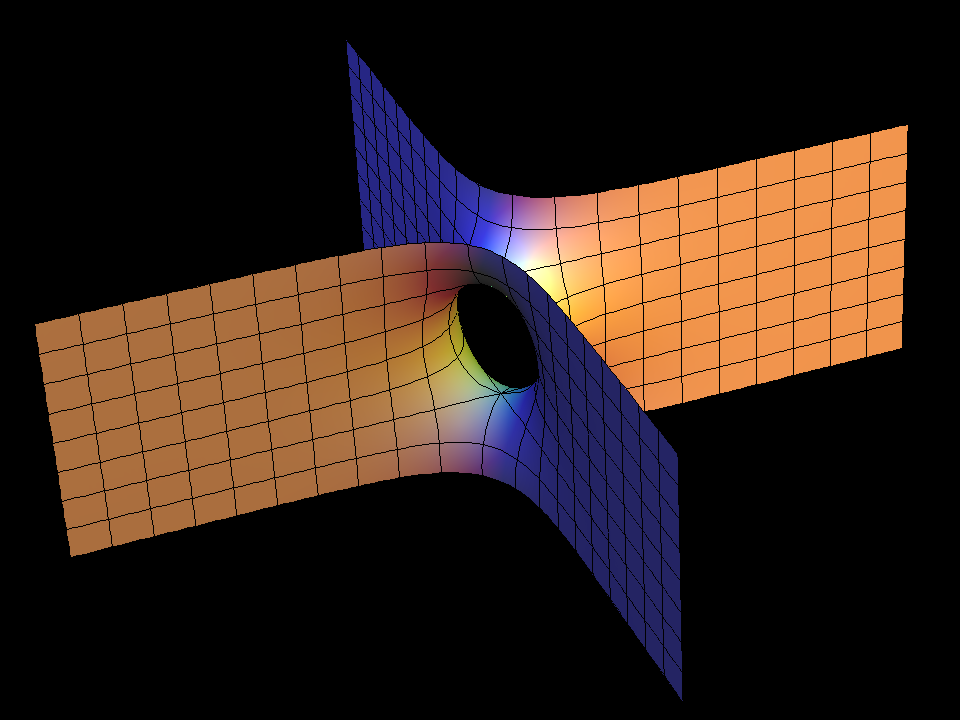
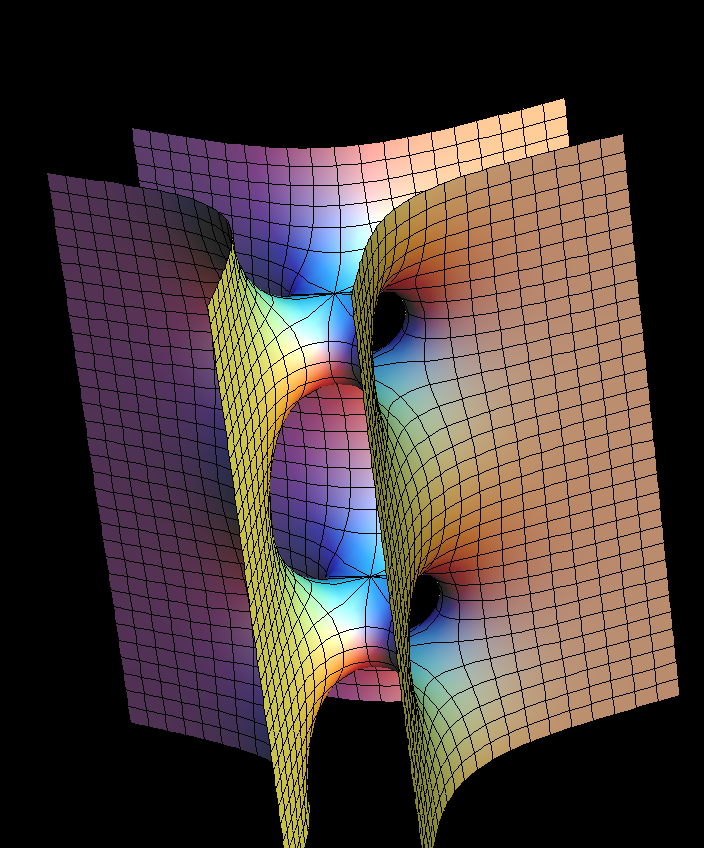
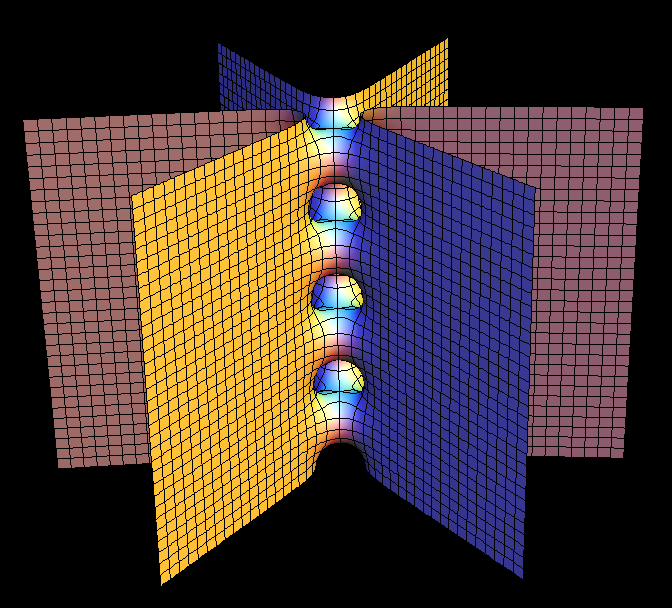
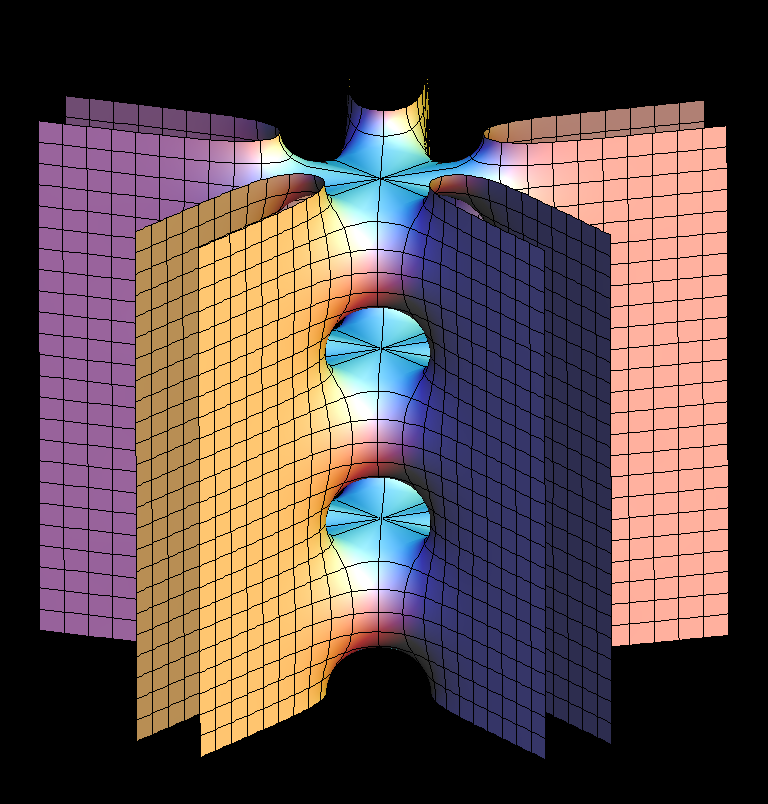
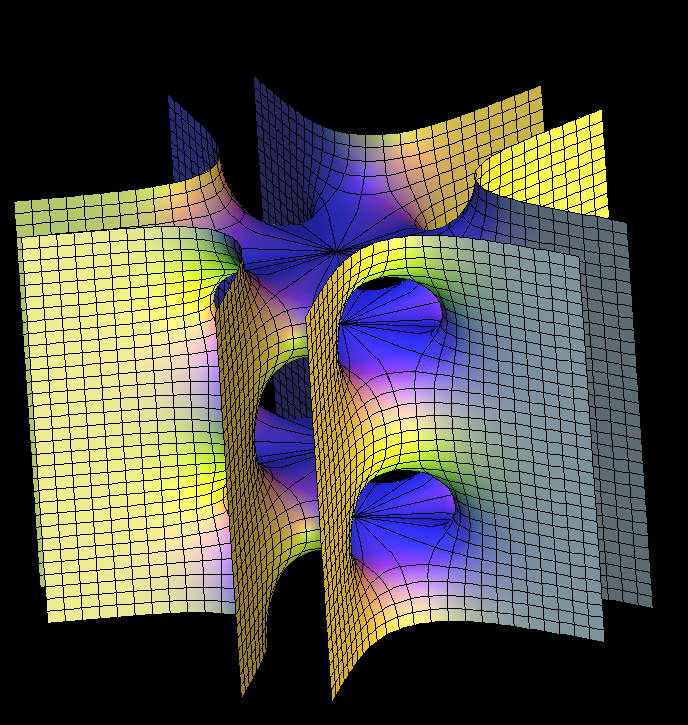
[see Scherk Surface]
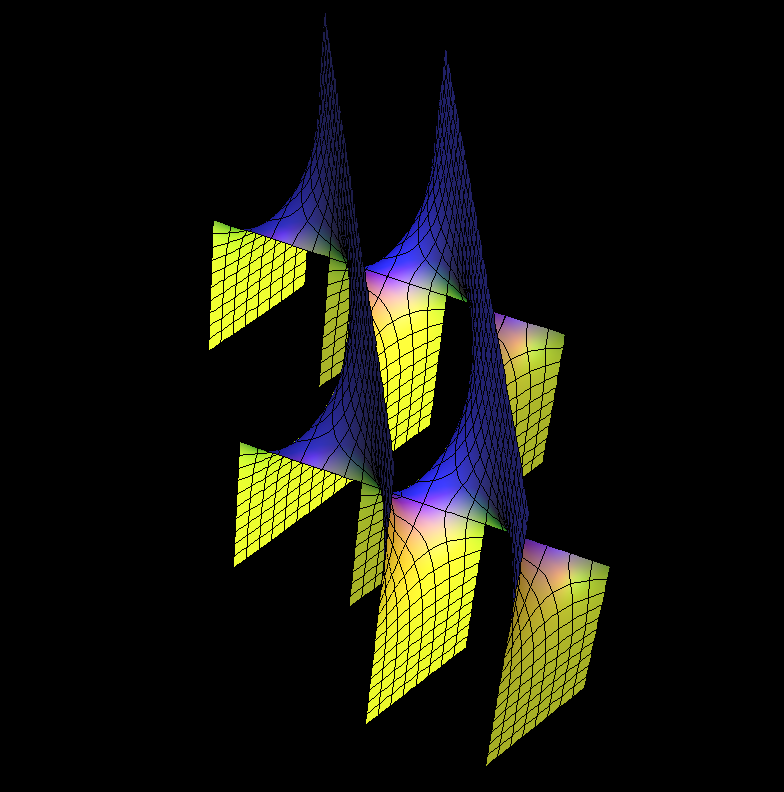
Plateau's problem is to show the existence of a minimal surface with a given boundary. The question was raised by Joseph-Louis Lagrange in 1760.
Physicist Joseph Plateau conducted extensive studies of soap films and formulated Plateau's laws which describe the structures formed by such films in foams. Plateau convinced mathematicians that Lagrange's problem probably has an answer.
For more, see Wikipedia Plateau's problem
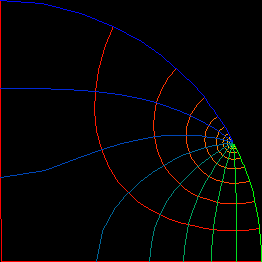
The so called “Weierstrass Integral” produces this surfaces by mapping pieces of the Gaussian plane into R^3. So far no parameter lines enter. For visualization one wants lines on the surface which support a 3-dimensional interpretation of the 2-dimensional image. Level lines have proved to be a good choice. The above grid on one quarter of the unit disk produces the parameter lines on the 4-winged saddle towers and their doubly periodic conjugates.
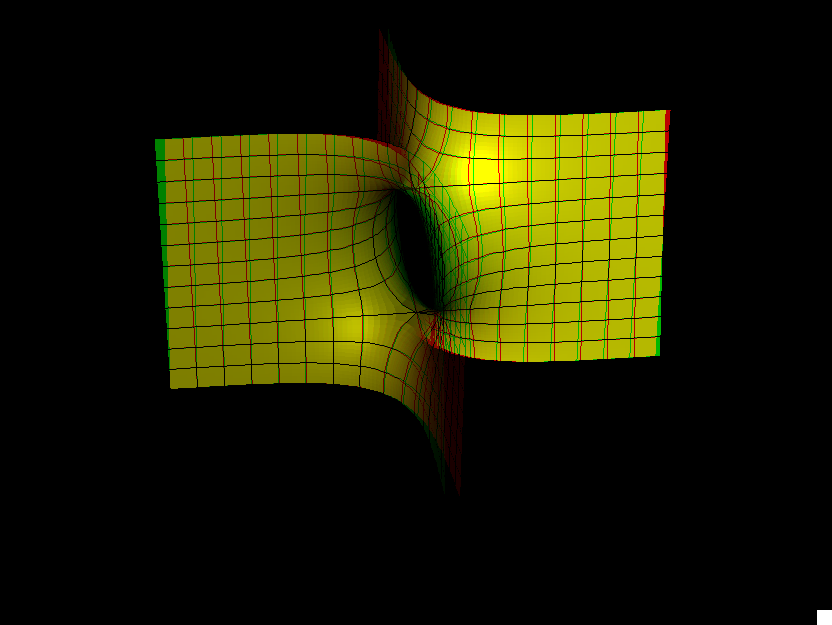
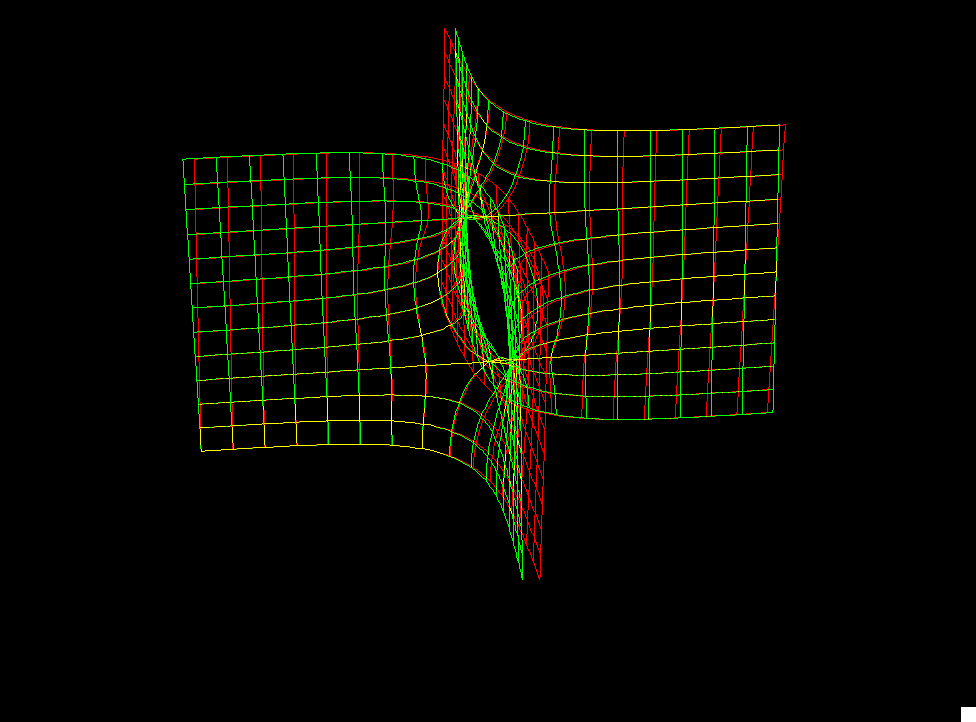
These examples generalize Scherk's conjugate pair of singly-periodic/doubly-periodic minimal surfaces. [see Scherk Surface]
The singly-periodic examples stay embedded if the dihedral symmetry (and with it the number of punctures) is increased (Gauss(z)=z^k , k=ee-1). The most symmetric ones (bb=0.5/ee) can be deformed by decreasing bb. See [K1], [K2] for more details.
These surfaces are parametrized by punctured spheres, but the Weierstrass integrals have periods, a vertical one in the singly periodic case, two horizontal ones for doubly periodic surfaces. The parameter lines extend polar coordinates around the punctures to the whole sphere---in these cases giving level lines on the surfaces.
The degree of dihedral symmetry is, of course, a discrete property, and it is controlled by the parameter ee. Thus, ee should be set to an integer (the default is 2). For each choice of ee, changing bb gives a one-parameter family of surfaces, of which the most symmetric member is obtained by setting bb = 0.5/ee. Try setting ee to 3 and 4, and bb to 0.333 and 0.25 respectively. The wings of the singly periodic SaddleTower surfaces become *parallel in pairs* if (for ee>2 ) one sets bb = 0.0825. These stay embedded for ee=3 and ee=4.
For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see either [KWH], or pages 192--217 of [DHKW].