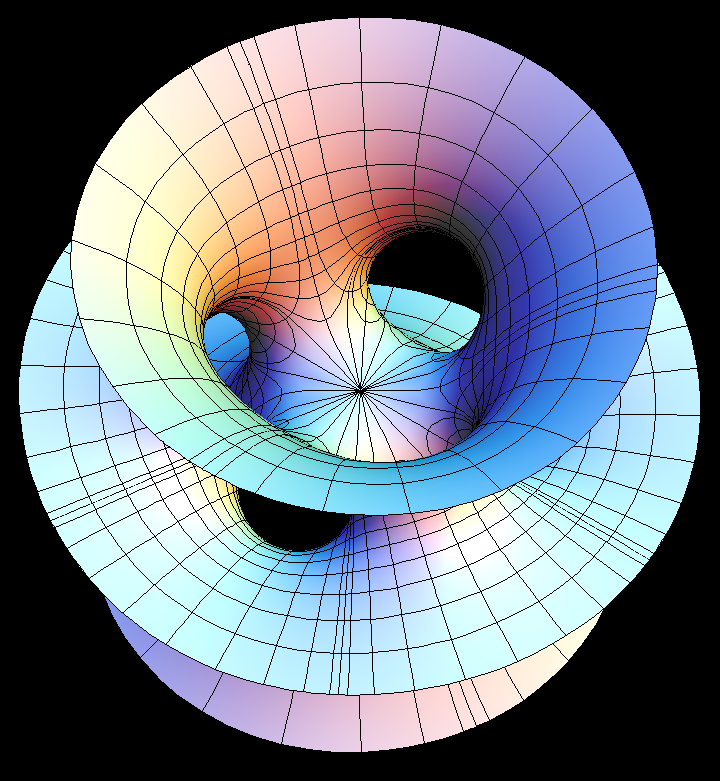

Costa-Hoffman-Meeks Surface is generailization of the Costa Surface to higher dihedral symmetry.
Costa-Hoffman-Meeks Surface with dihedral symmetry n has genus n-1.
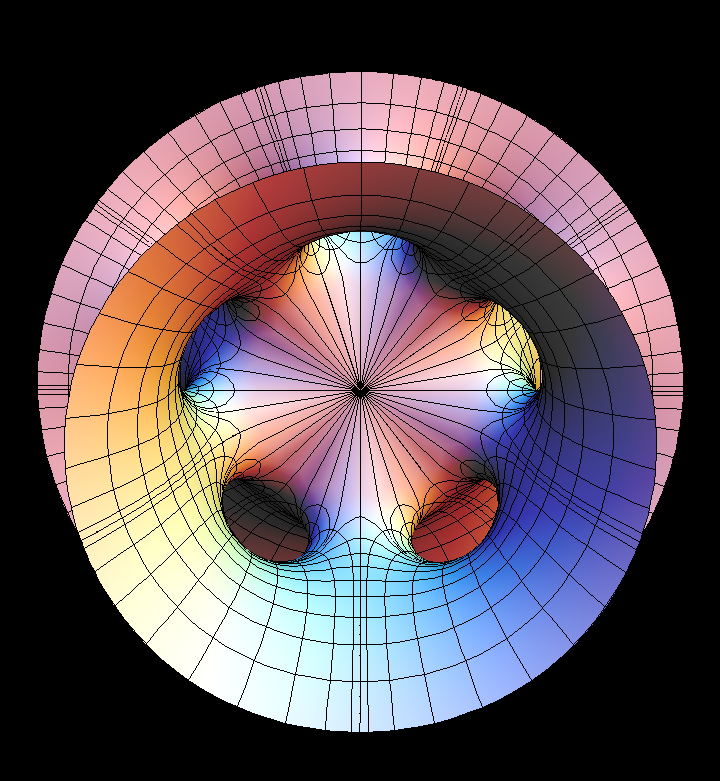
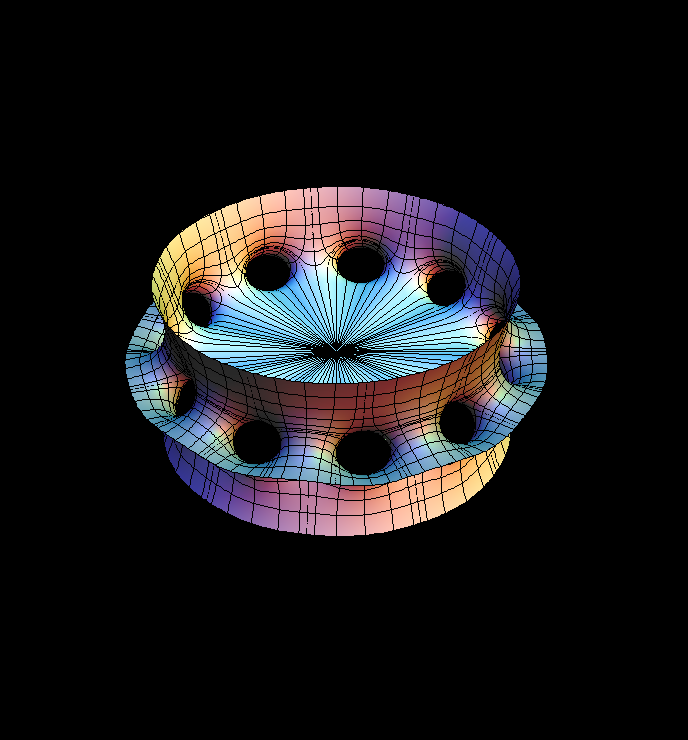

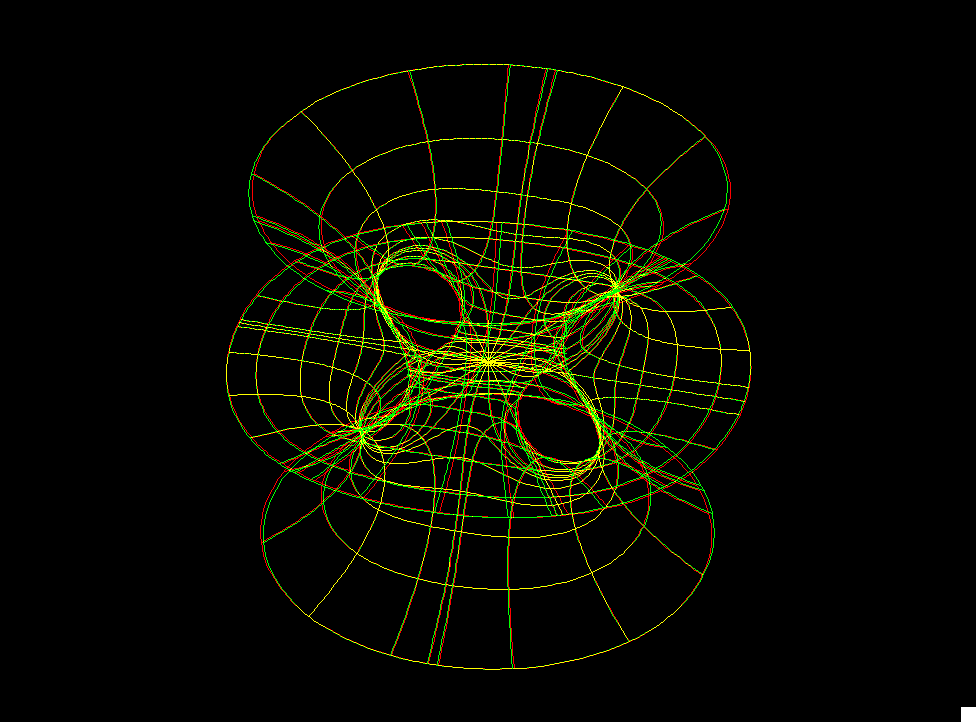
The original Costa Surface was responsible for the rekindling of interest in minimal surfaces in 1982. It is a minimal EMBEDDING of the 3-punctured square Torus. Its planar symmetry lines cut this surface into four conformal squares and the two straight lines through the saddle are the diagonals of these squares. Because of the emphasis on the symmetries, our formulas are taken from [K2.]
The Costa-Hoffman-Meeks surfaces are generalizations of the Costa Surface; their genus grows as the dihedral symmetry (controlled by dd) is increased. The underlying Riemann surfaces are tesselated by hyperbolic squares with angles pi/k, (k = 2,3, ...).
The Gauss map of such a surface is determined by its qualitative properties only up to a multiplicative factor cc which we suggest for the morphing (as in the Chen Gackstatter case). It closes the period (at cc0) with an intermediate value argument.
For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see either [KWH], or pages 192--217 of [DHKW].