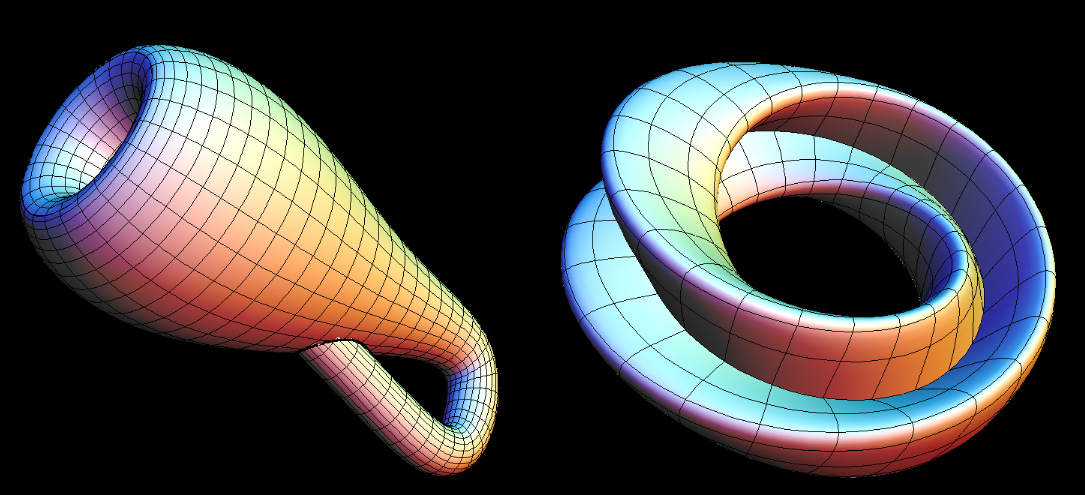
They cannot be deformed into each other.
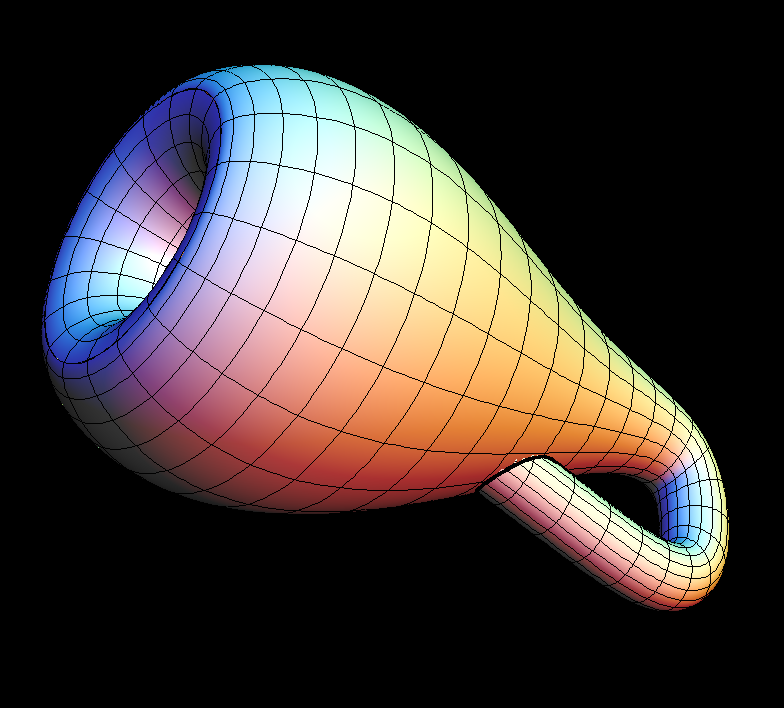

Klein Bottle
Hermann Karcher
Parametric Equations for the Twisting Klein Bottle
x = (aa + cos(v / 2) * sin(u) - sin(v / 2) * sin(2 * u)) * cos(v)
y = (aa + cos(v / 2) * sin(u) - sin(v / 2) * sin(2 * u)) * sin(v)
z = sin(v / 2) * sin(u) + cos(v / 2) * sin(2 * u)
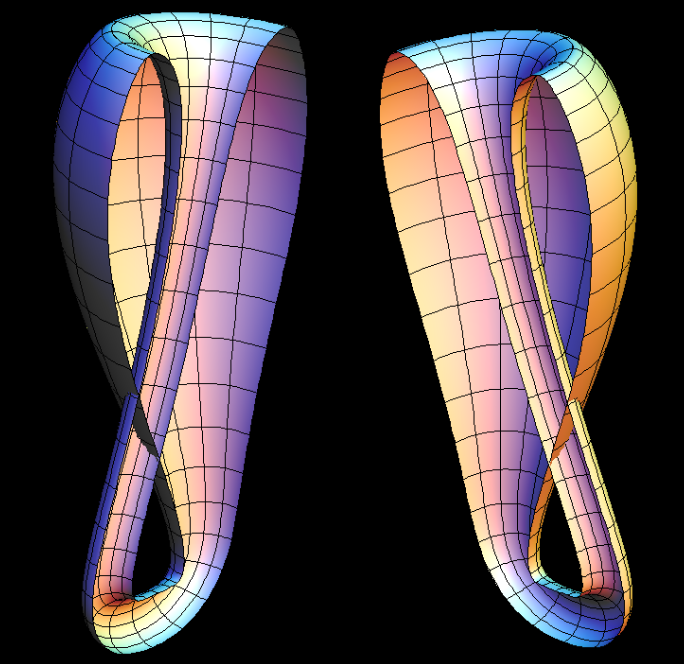
See the Mobius Strip first.
The non-orientable surfaces are "one-sided",
and this concept can best be understood if one starts from a Mobius Strip.
Imagine that we modify a Torus by rotating a figure-eight instead of a
circle. If we color the two sides of this surface differently then one
loop of the figure-eight has one color, the other loop the other color.
(One can make such a surface in the Surface Category, by taking the
Lemniscate as the meridian curve after choosing "User Defined (Rotation)"
from the Surface menu. (This is in fact is the default meridian. )
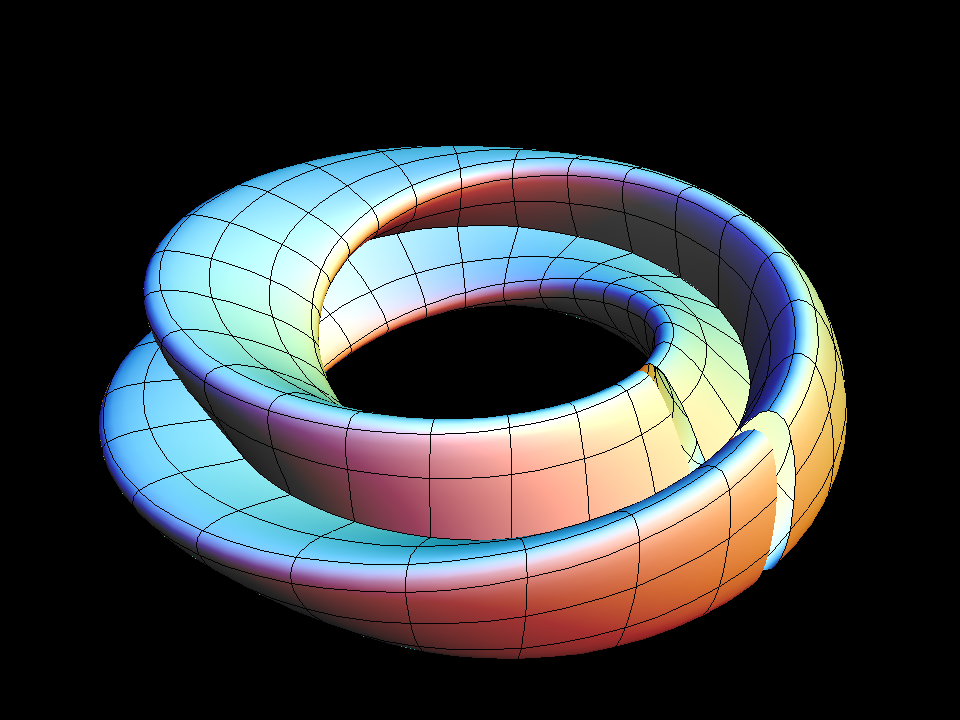
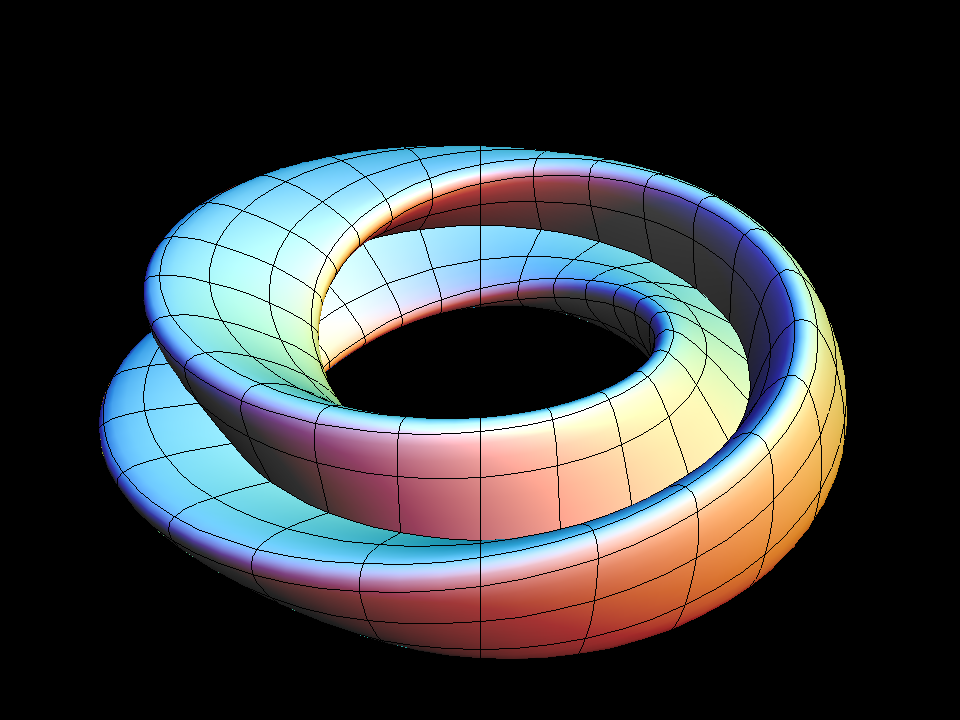
The default Klein Bottle is obtained by one further modification:
Rotate the meridian figure-eight in its plane by 180 degrees as the
curve is being rotated 360 degrees about the axis of rotation. One can
see the figure-eight better if in "Set u,v ranges" one sets vmin = 0.5.
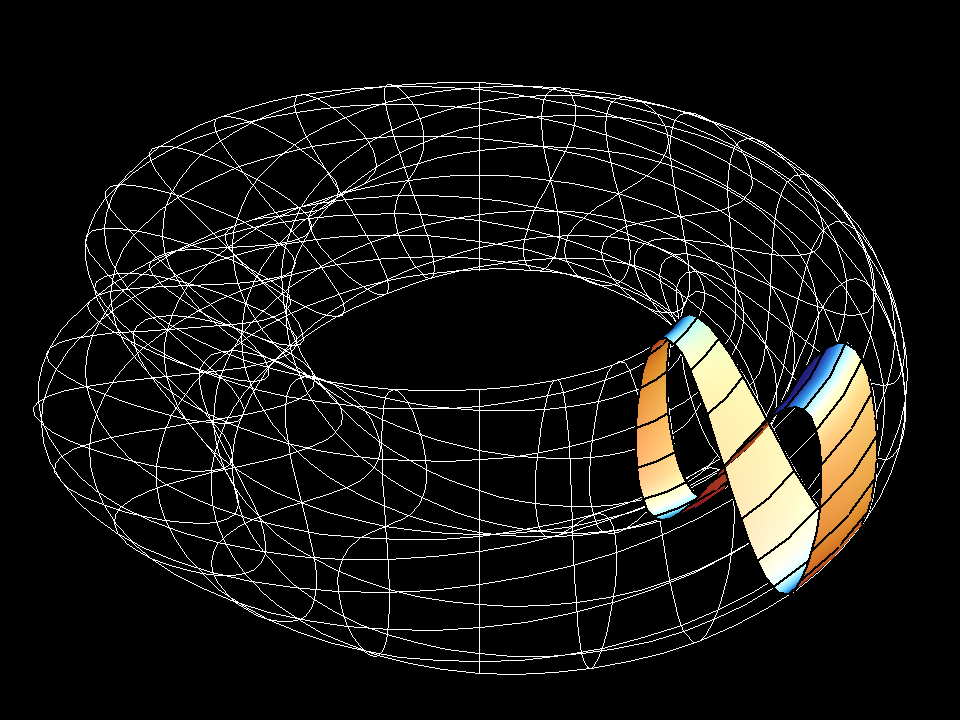
Use ``Distinguish Sides by Color'' in this cut open view. One can see this
in a morph with
aa= 3, umin=0, umax=2 * π, vmin=0, 0.5 < umax < 2 * π.
The default morph starts from the Mobius Strip
-0.4 < u < 0.4, 0 < v < 2 * π, aa = 3
and increases the width of the Mobius Strip until it closes
to the Klein Bottle at - π < u < π.
There are in fact three different kinds of Klein Bottles which
cannot be deformed into each other:
(i) The present one, where the figure-eight rotates to the left in its plane;
(ii) The mirror image of the present one, where the figure-eight rotates
clockwise;
(iii) a Klein Bottle with mirror symmetry, glass models are frequently made.