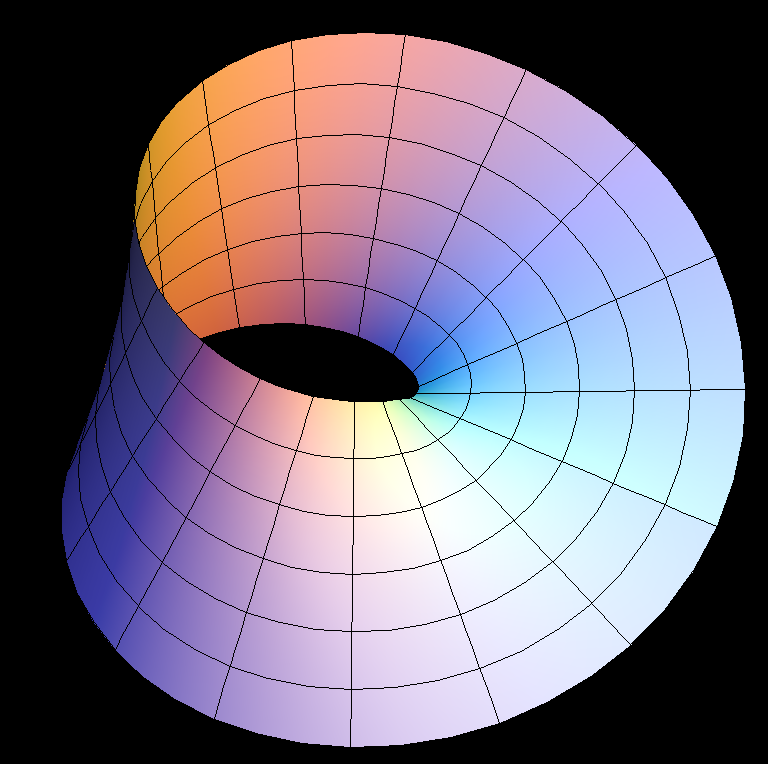


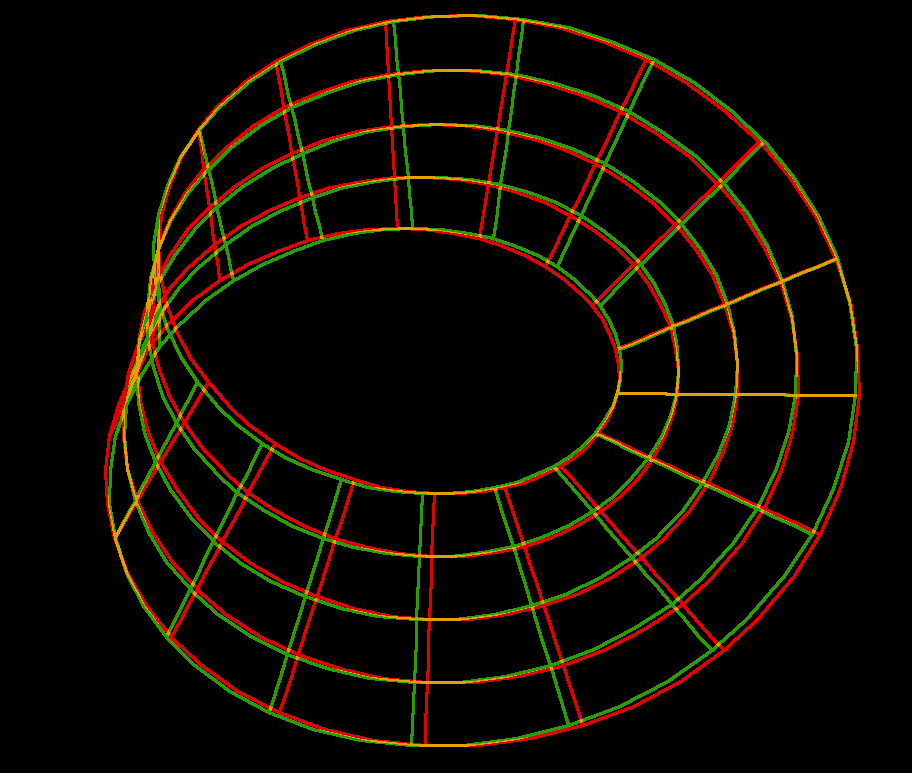
Parametric Equations
x = aa * (cos(v) + u * cos(v / 2) * cos(v)) y = aa * (sin(v) + u * cos(v / 2) * sin(v)) z = aa * u * sin(v / 2)
The Mobius Strip is perhaps the most famous of the one-sided or “non-orientable” surfaces.
A Mobius Strip can be found on any non-orientable surfaces. To see one on the Klein Bottle, select from the Settings menu “Set t,u,v Ranges” and put umin = - 0.4, umax = + 0.4 . On the Boys surface, there are even two different kinds. To see one with three half-twists, change to umin = 0.9; this is a band with the “equator” of the Boys surface as its centerline. Bands with meridians as center curves are ordinary Moebius bands. To see one, change the u,v-ranges to umin = -0.998, vmin = 6.1 :
(On the Steiner Surface and on the Crosscap, one can also find Mobius Strips. However these are not embedded and so are not easily recognizable. In math jargon, these surfaces are not immersed and there is a singularity on the Moebius band.)