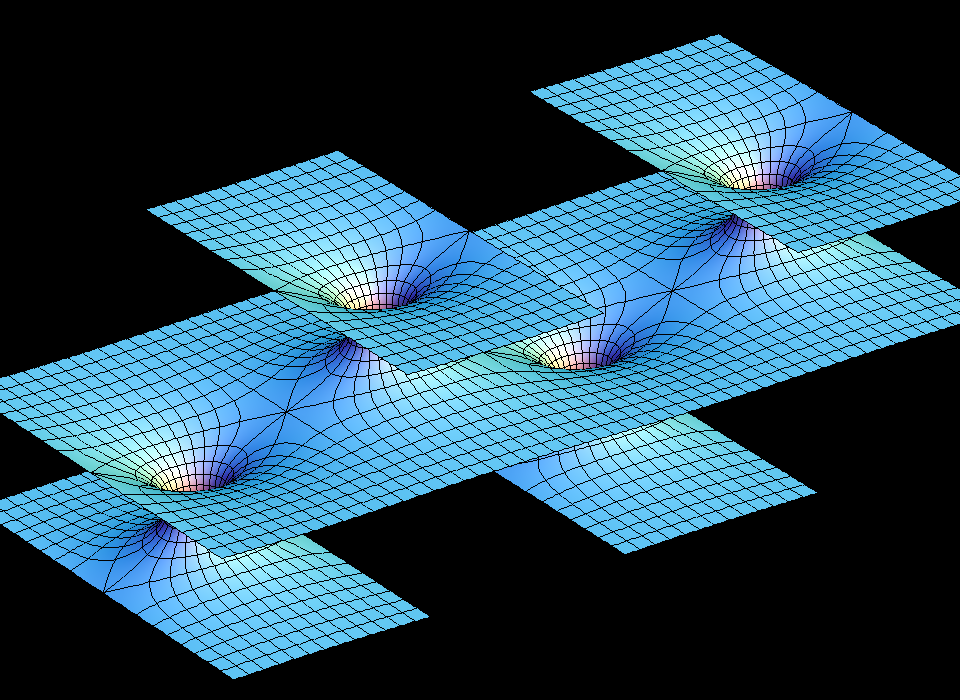

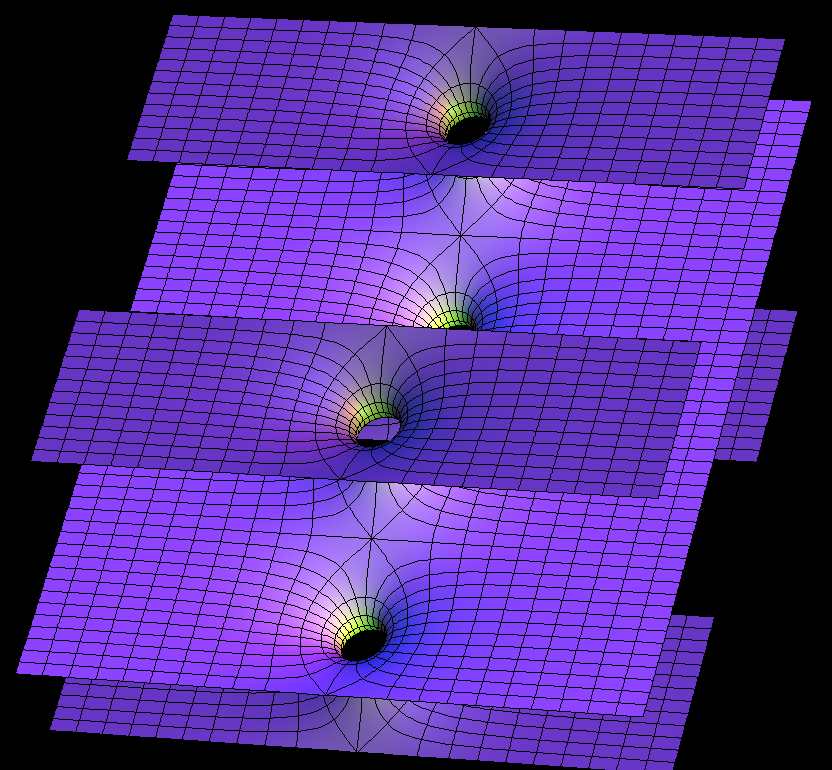
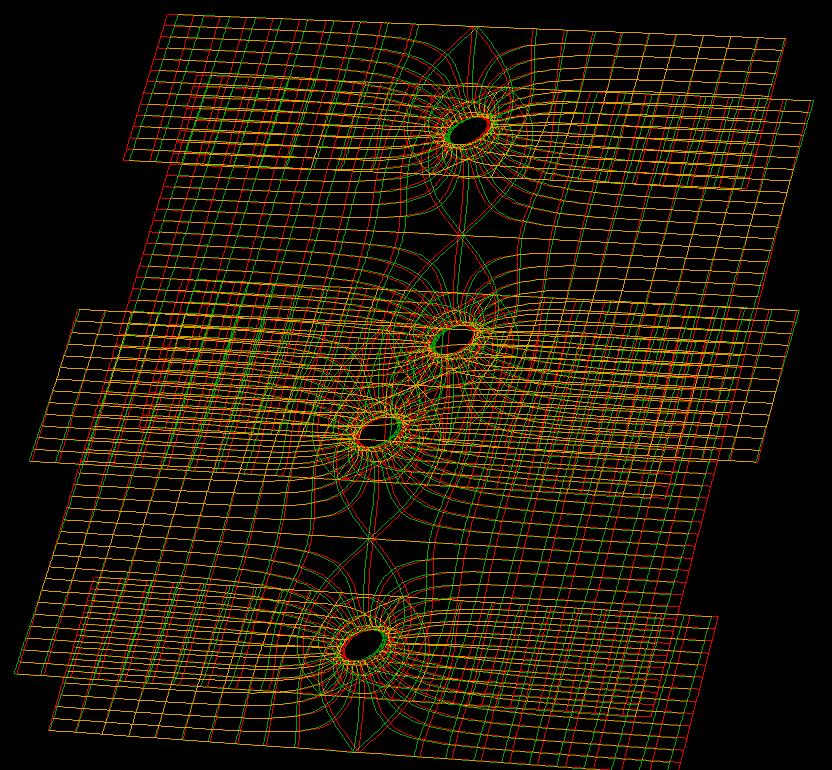
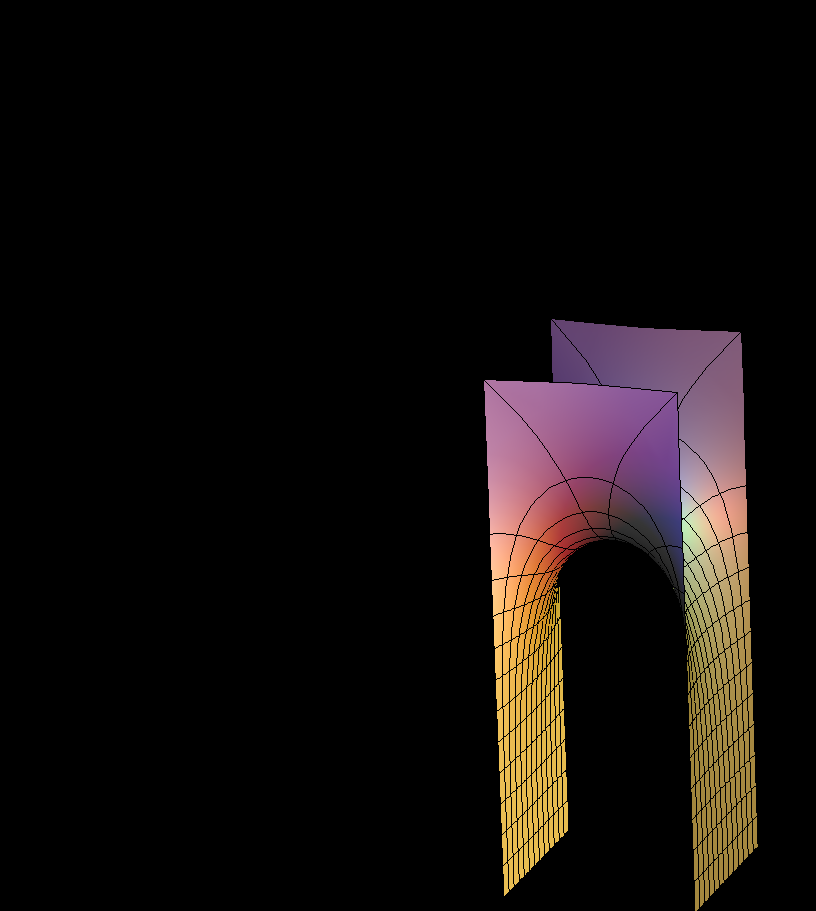
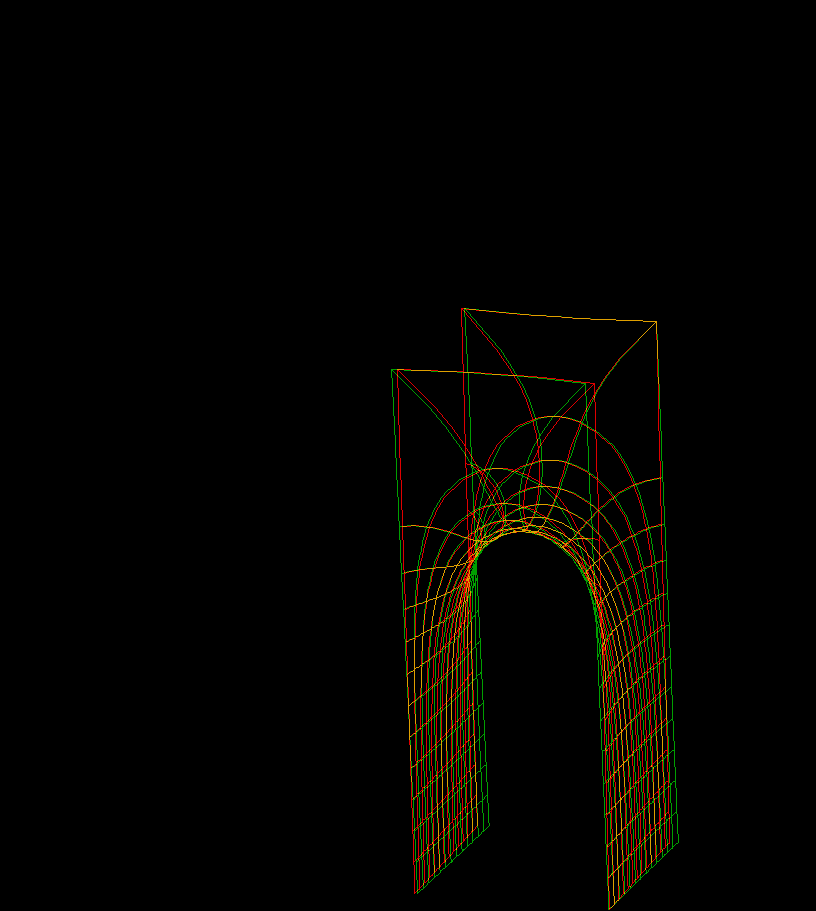

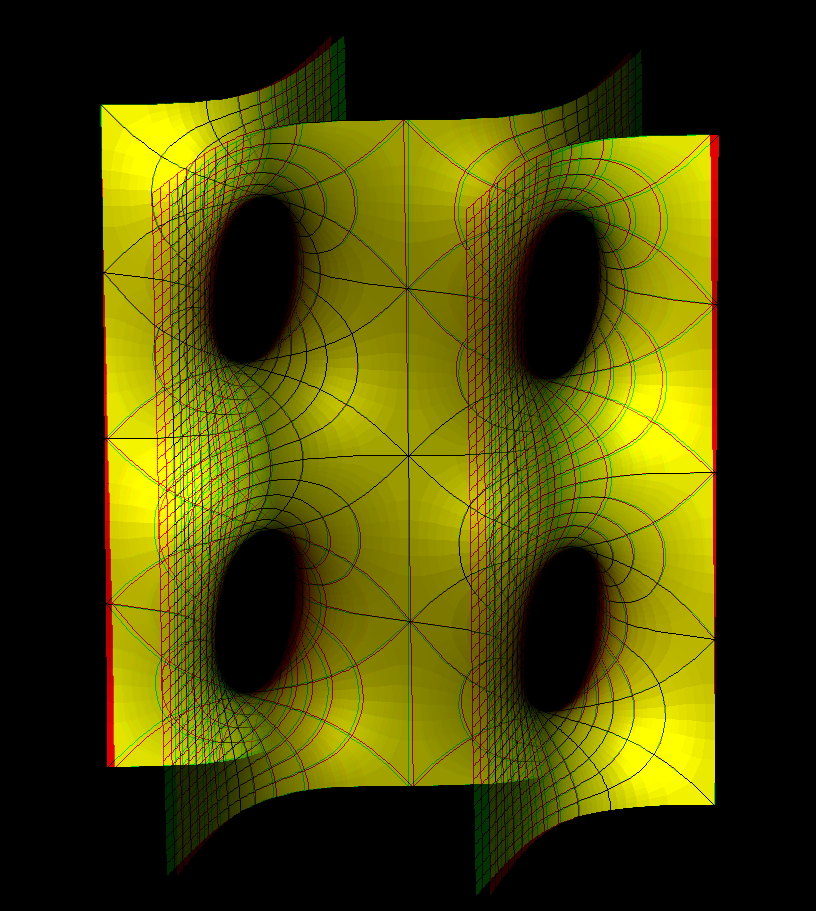
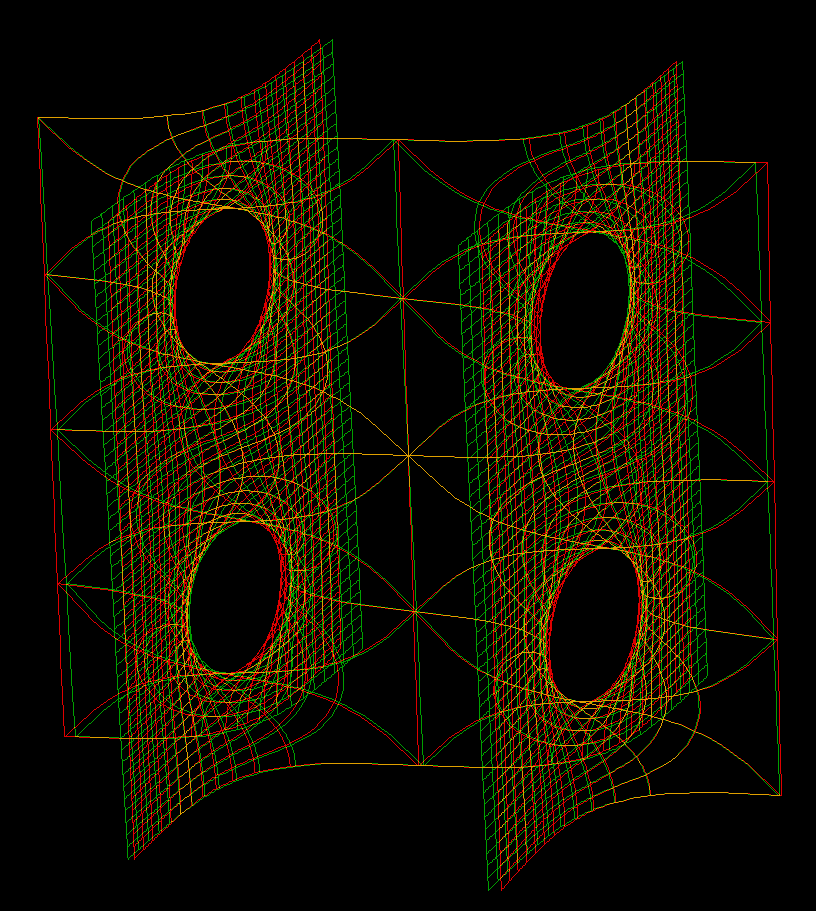

These families are parametrized by 4-punctured rectangular tori; they and their conjugates are embedded.
For the visual appearance of these surfaces it is particularly important that the punctures are centers of polar coordinate lines. Formulas are taken from [K1] or [K2]. The Gauss maps for these surfaces are degree 2 elliptic functions. The cases shown are particularly symmetric, the zeros and poles of the Gauss map are half-period points and the punctures are there. In the case of Karcher JD Saddle tower, the diagonal of the rectangular fundamental domain joins the two zeros, and in the Je-case it joins a zero and a pole of the Gauss map.
Under suitable choices of the modulus of the Torus these surfaces look like a fence of Scherk Saddle Towers — with a vertical straight line ( Karcher JE case), respectively a planar symmetry line ( JD case), separating these towers. The conjugate surfaces look qualitatively the same in the JD-cases and like a checkerboard array of horizontal handles between vertical planes in the JE-cases.
For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see either [KWH], or pages 192--217 of [DHKW].