Catenoid Fence

Three fundamental domains connected by rather fat handles.

Three fundamental domains connected by very thin handles. These almost-catenoids are much rounder than in the previous case of fat handles.

These images show always the same surface. Only larger portions of the half-catenoid-parts of the surface are computed. The two “almost catenoids” are congruent. One of them is a fundamental domain for the translation symmetries. In the theory of minimal surfaces one learns that a half-catenoid grows to infinity like a plane so that - contrary to the first impression - only one “point” at infinity is missing. The fundamental domain is therefore only a tube with a bulge in the middle and two points of the bulge are missing. Mathematiicians say that the translational symmetries “identify” the two boundary curves of the tube and make it into a torus.

The minimal surfaces of this animation are all different: The size of the “handle” which connects the two almost-catenoids and the size of the waist of the almost-catenoids change their ratio from surface to surface. This family of minimal surfaces was the first one with a “designed handle”. The Skew 4-noid family suggested that these surfaces might exist. For the construction one needed to find the (“elliptic”) functions which, when put into the “Weierstrass representation”, gives these surfaces.

catenoid fence st

catenoid fence sw

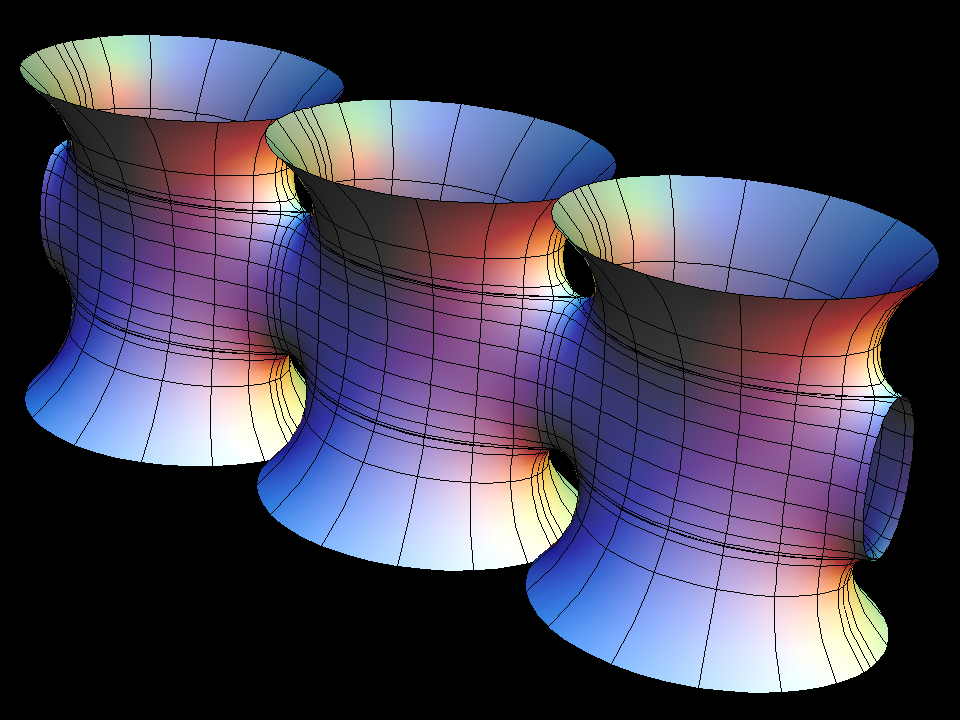
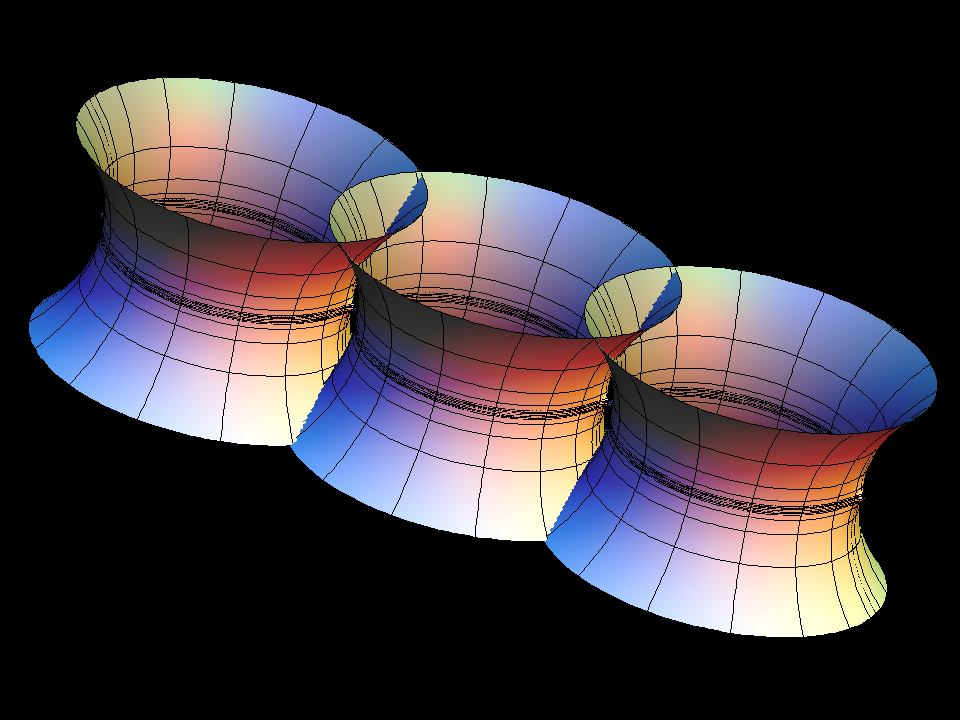
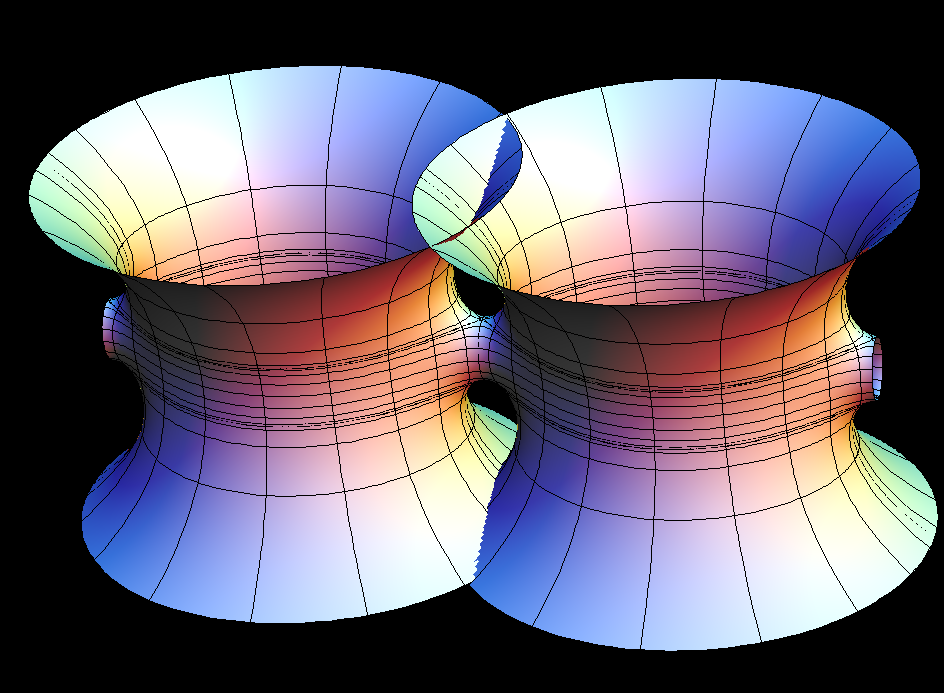
These singly periodic surfaces are parametrized (aa) by rectangular tori; our lines extend polar coordinates around the two punctures to the whole Torus. The surfaces look like a fence of catenoids, joined by handles; they were made by Karcher and Hoffman, responding to the suggestive skew 4-noids. The morphing parameter aa is the modulus (a function of the length ratio) of the rectangular Torus.

Formulas are taken from:

Construction of Minimal Surfaces, H Karcher , in “Surveys in Geometry”, Univ. of Tokyo, 1989, and Lecture Notes No. 12, SFB 256, Bonn, 1989, pp. 1 — 96.

For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see:

[KWH] H. Karcher, F. Wei, and D. Hoffman, The genus one helicoid, and the minimal surfaces that led to its discovery, in “Global Analysis in Modern Mathematics, A Symposium in Honor of Richard Palais' Sixtieth Birthday”, K. Uhlenbeck Editor, Publish or Perish Press, 1993
[DHKW] U. Dierkes, S. Hildebrand, A. Kuster, and O. Wohlrab, Minimal Surfaces I, Grundlehren der math. Wiss. v. 295 Springer-Verlag, 1991

Catenoid Fence

Related Surface of Catenoid