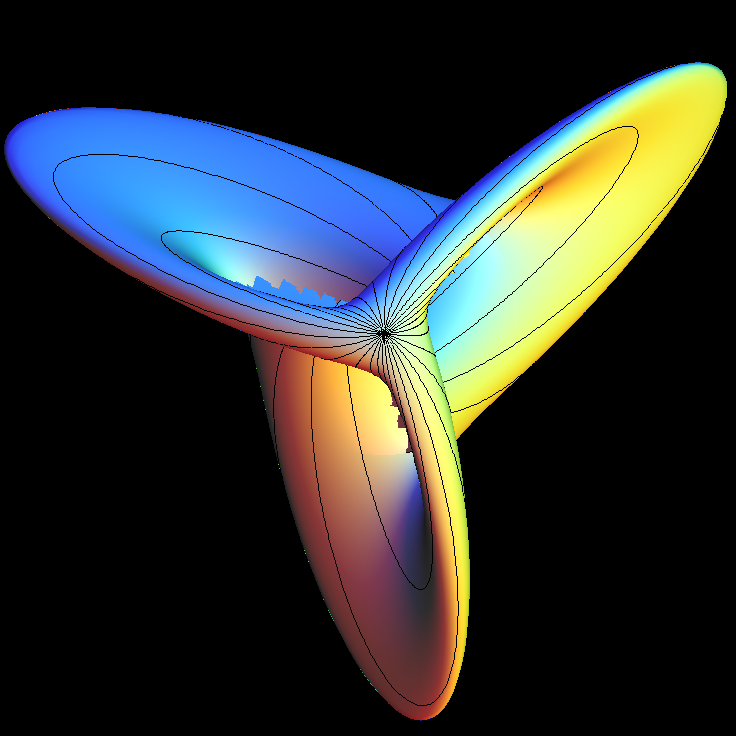
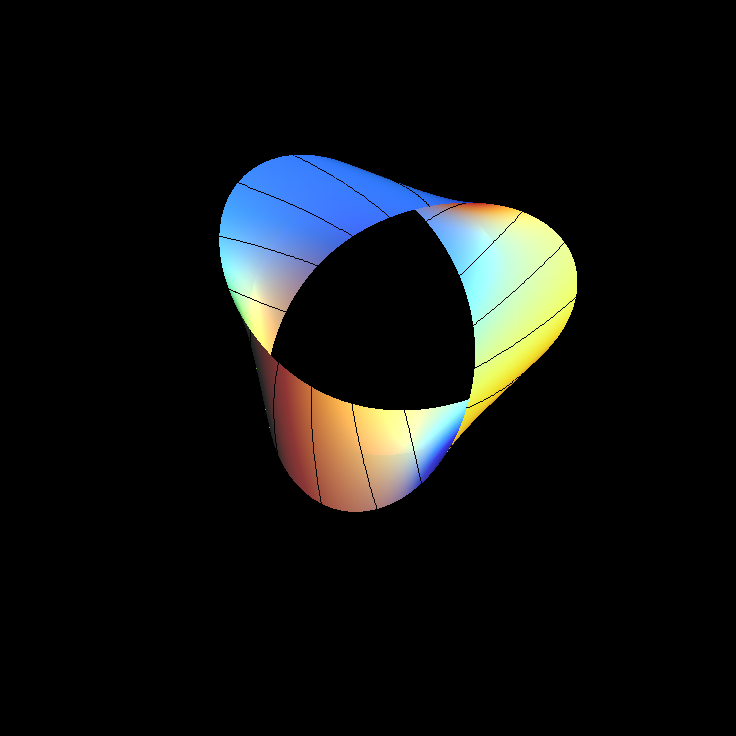
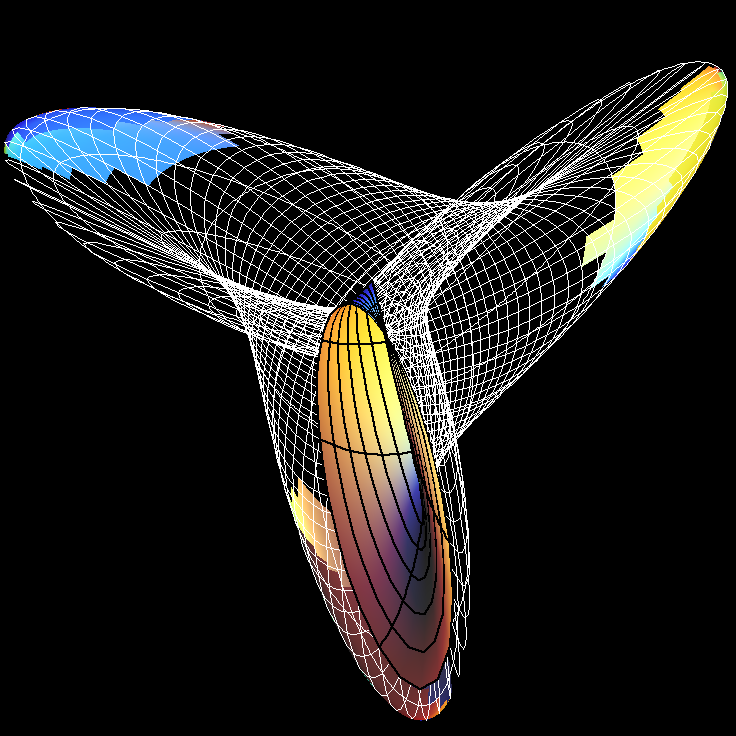
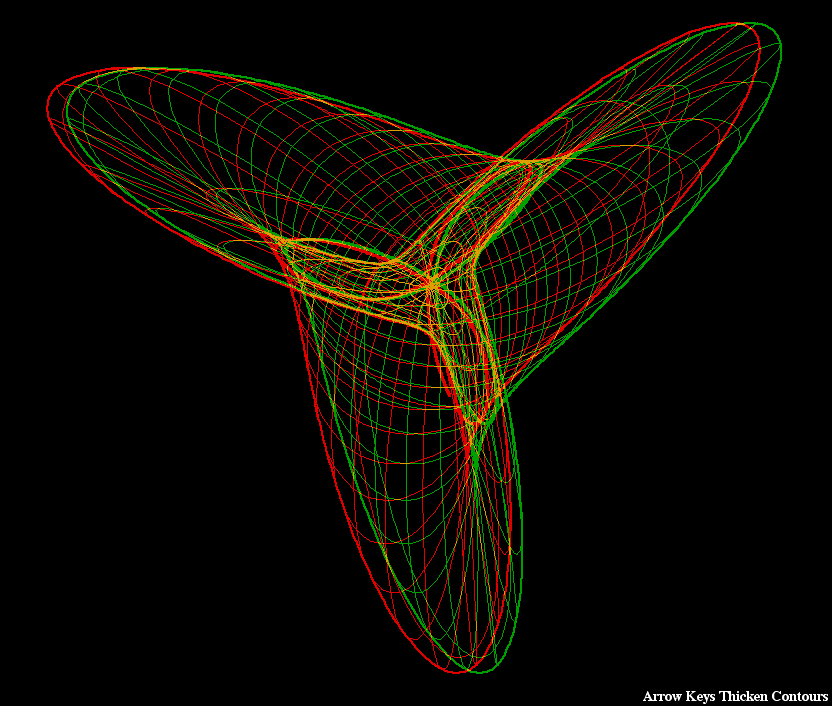
Boy's Surface (Apery)

Boys Surface (After Apery)

The Boys Surface is really a family of surfaces. Boys, in his dissertation under Hilbert, constructed an immersion of the projective plane. Being nonorientable implies that no embedding is possible. Boys Surface has besides its self-intersection curves only one more serious singularity, namely a triple point. His construction was topological.

Apery found algebraically embedded "Boys Surfaces". They carry one-parameter families of ellipses.

The Bryant-Kusner Boys Surfaces are obtained by an inversion from a minimal surface in R^3. This minimal surface is an immersion of S^2 - 6 points such that antipodal points have the same image in R^3. The six punctures are three antipodal pairs, and the minimal surface has so called "planar ends" at these punctures. In this context it is important that the puncture in the inversion of a planar end can be smoothly closed by adding a point. The closing of the three pairs of antipodal ends thus gives a triple point on the surface obtained by inversion.

The formula for Apéry's immersion is:

P.x := (2/3)*(cos(u)*cos(2*v)+sqrt(2)*sin(u)*cos(v))*cos(u) / (sqrt(2) - sin(2*u)*sin(3*v));
P.y := (2/3)*(cos(u)*sin(2*v)-sqrt(2)*sin(u)*sin(v))*cos(u) / (sqrt(2)-sin(2*u)*sin(3*v));
P.z := sqrt(2)*cos(u)^2 / (sqrt(2) - sin(2*u)*sin(2*v));