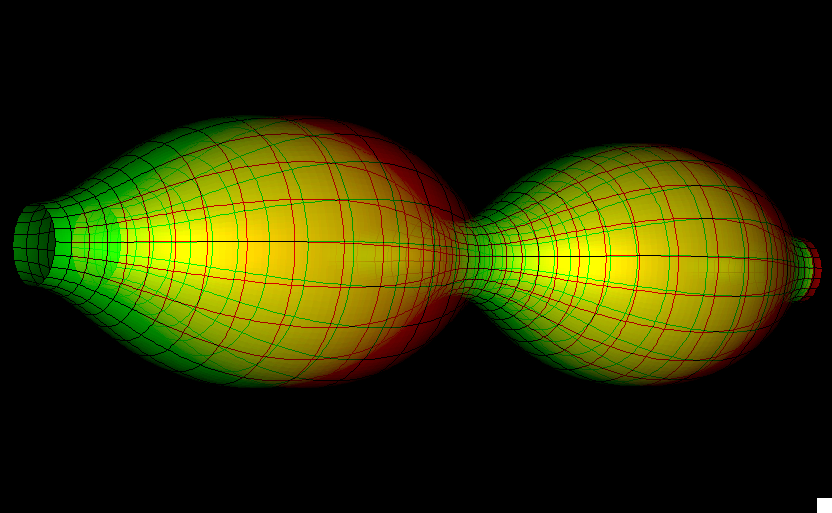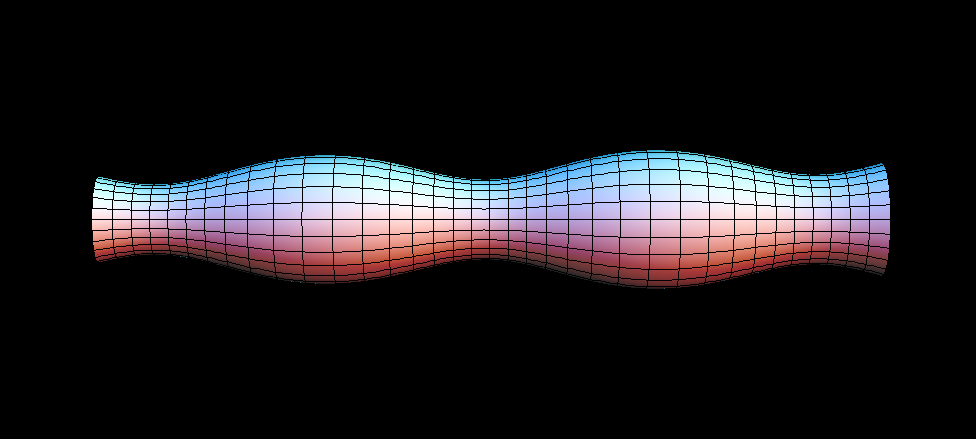

Unduloid describes a family of surface of revolution. Let a conics section roll on a line. Its focus traces out a curve. This curve revolved around the line generates the unduloid. The above image shows an unduloid where the rolling curve is an ellipse. It has a mean curvature of 1. If the rolling curve is a parabola, a catenoid will be generated, and has mean curvature of 0.
A soap film is a constant mean curvature surface, if the pressure difference between both sides is constant. (If this constant is zero the surface is called minimal surface)