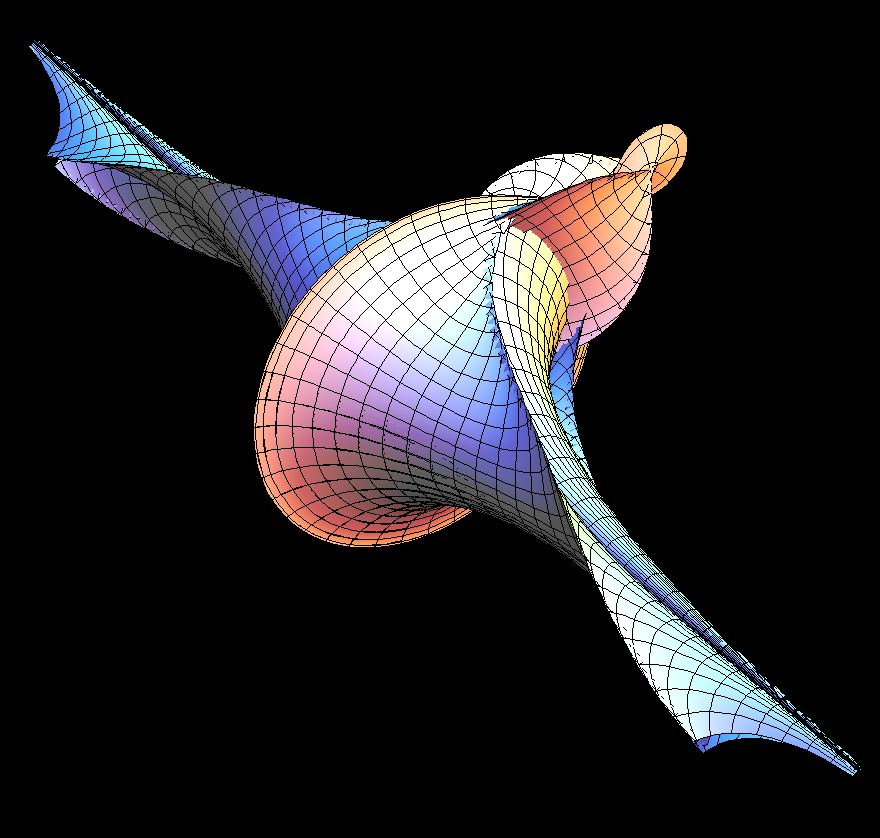
Three-Soliton Surface

Three-Soliton Surface means: a surface family of Gauss curvature K = -1 which depends on three constants a, b, c; the word “soliton” refers to solutions of the Sine-Gordon Equation from which the surfaces are constructed; these solitons q(a,b,c; u,v) also depend on a, b, c; as functions of (u,v) they are defined and without singularities for all (u,v) in R^2.

Negative curvature can be seen in images: No tangent plane leaves the surface locally on one side but each tangent plane intersects the surface. The intersection curve has a double point where the tangent plane touches and the angle between the two tangents at the double point is q(a,b,c; u,v). The sharp rims of the surfaces occur where sin(q) = 0.

All 3-soliton surfaces have many selfintersections; to get interpretable images the (u,v)-range is restricted to a small rectangle (contained in |u|,|v| ≤ 10).

three-soliton different — A 3-soliton surface with a = 0.5, b = 0.2, a = 0.8.

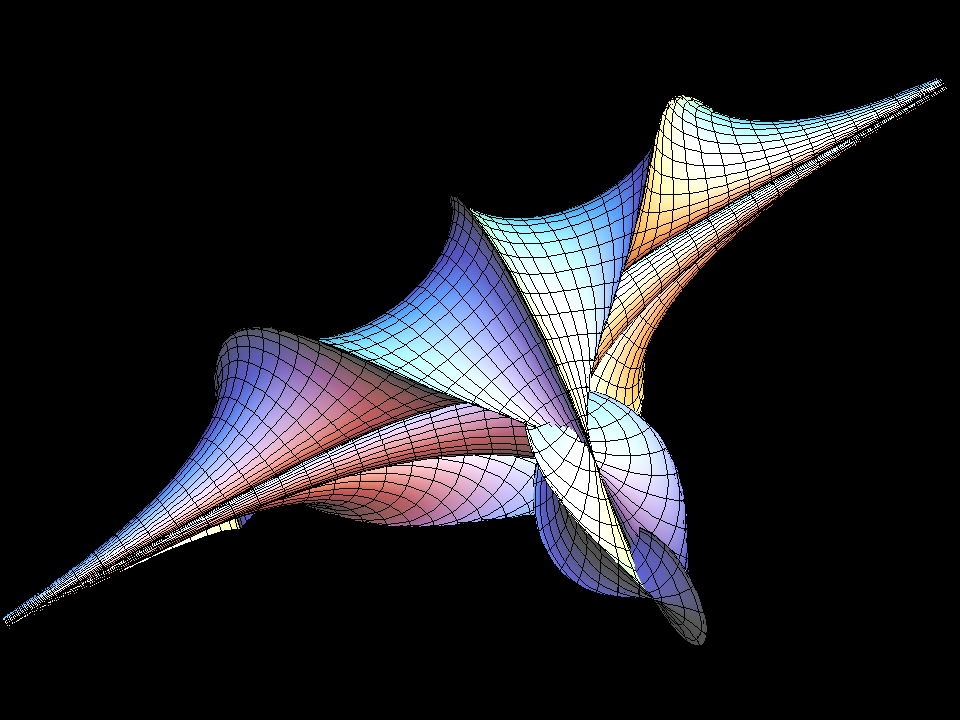
three-soliton equal2 — A 3-soliton surface where the three constants are close, a = 0.5, b = 0.51, c = 0.49. The formulas do not allow equal constants, although the limit surfaces exist.

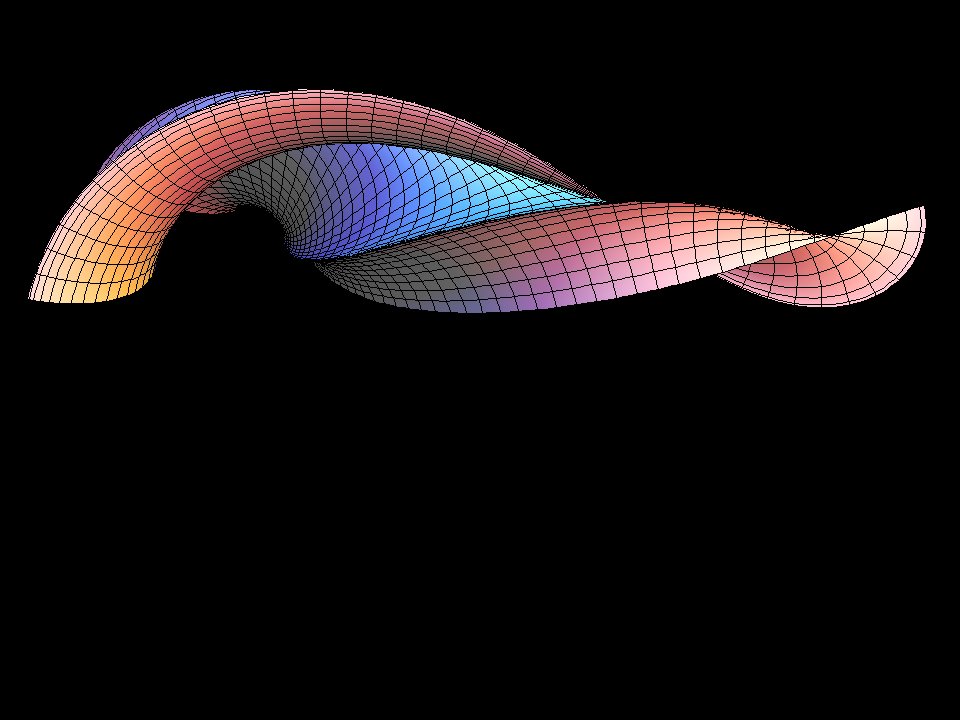
three-soliton grow 001 — In this sequence the parameter v grows. constants (a,b,c) = (0.5, 0.51, 0.49).

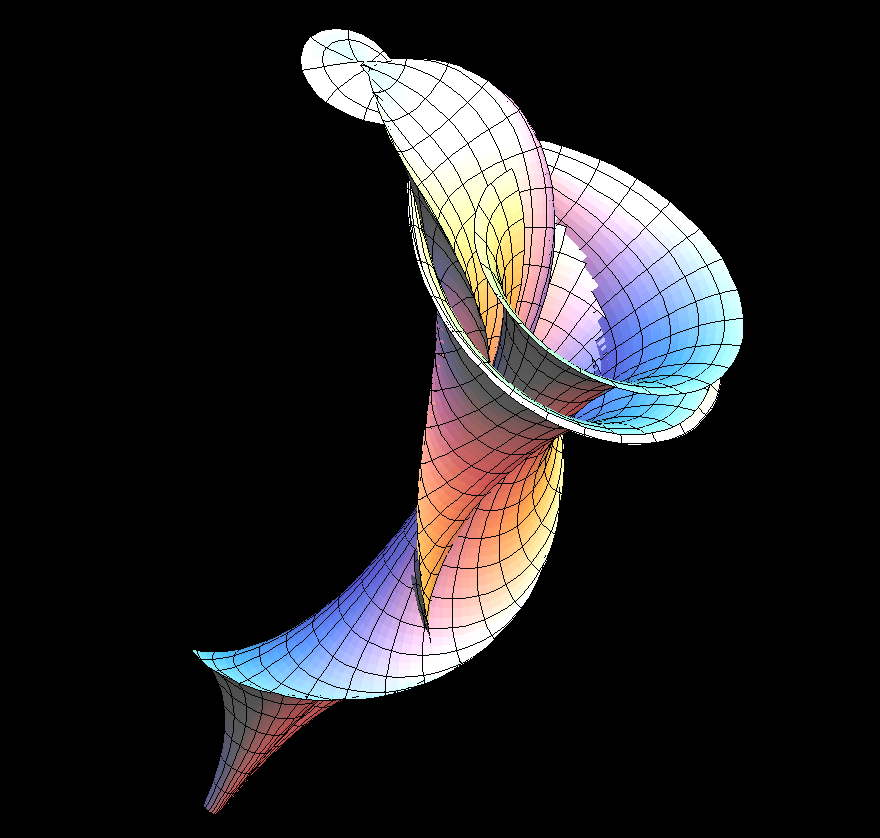
three-soliton half-more-v — The range of u is half of the previous squence, -7 ≤ u ≤ 0, but the range of v is larger than in the previous sequence, -7 ≤ v ≤ 9.

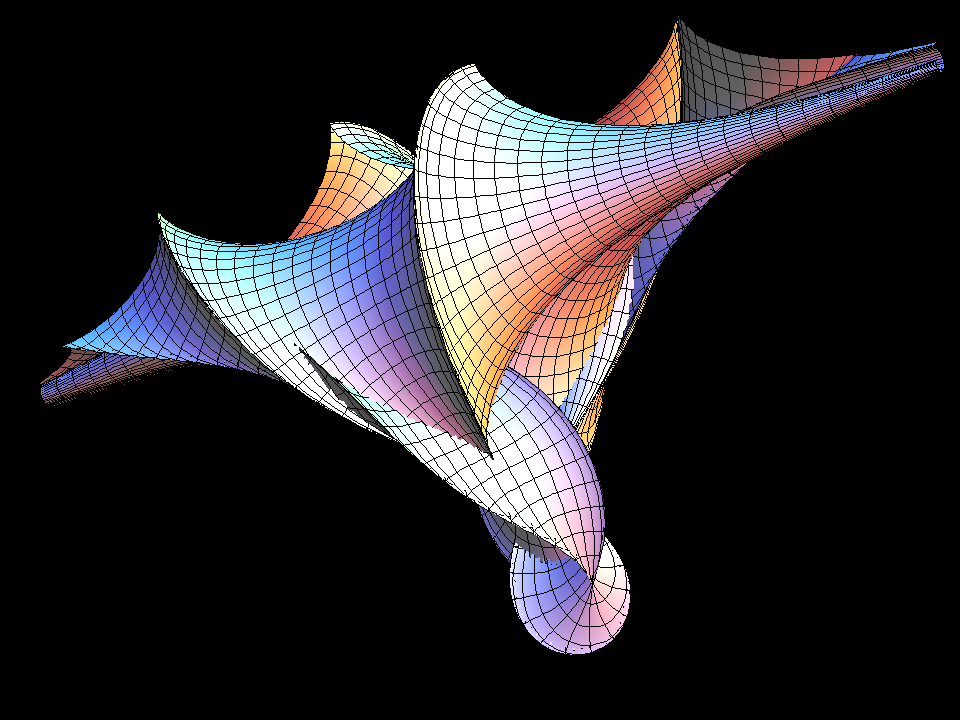
three-soliton morphE 001 — The (u,v)-domain is fixed, a = 0.5, 0.29 ≤ b ≤ 0.79, 0.31 ≤ c ≤ 0.81. To distinguish the deformatio from a rotation: observe the changing intersection pattern and the orientation of the protruding disk (or “hands”) relative to the long axis of the surface.

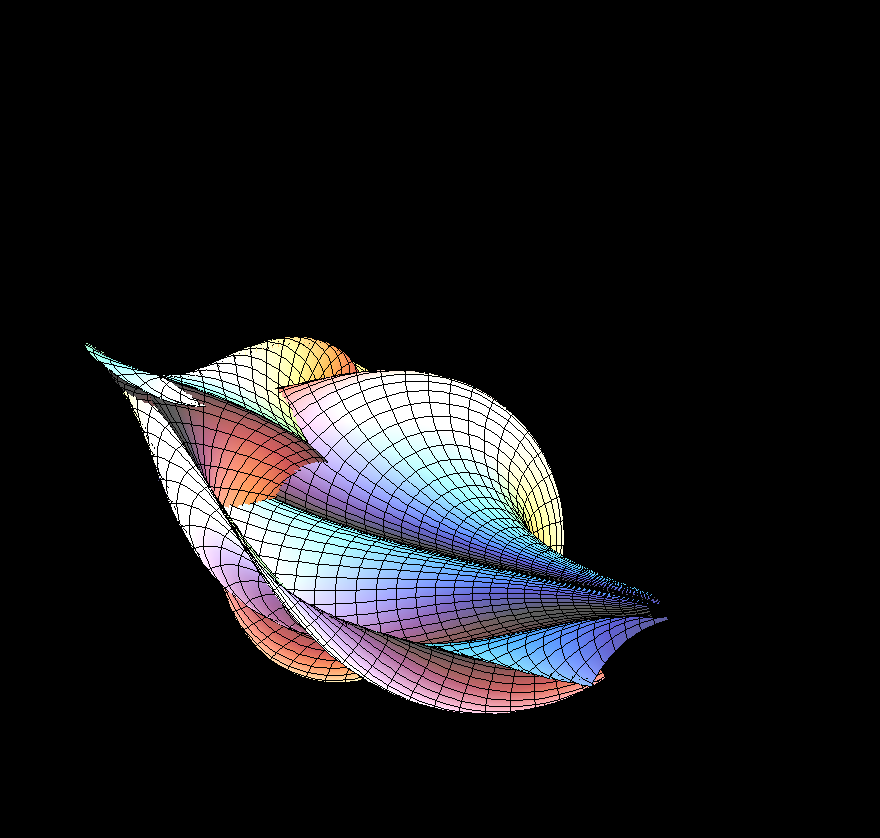
three-soliton morphF 001 — Same deformation as before, but from a different perspective. (Again, observe intersection pattern and orientation of the hands.)

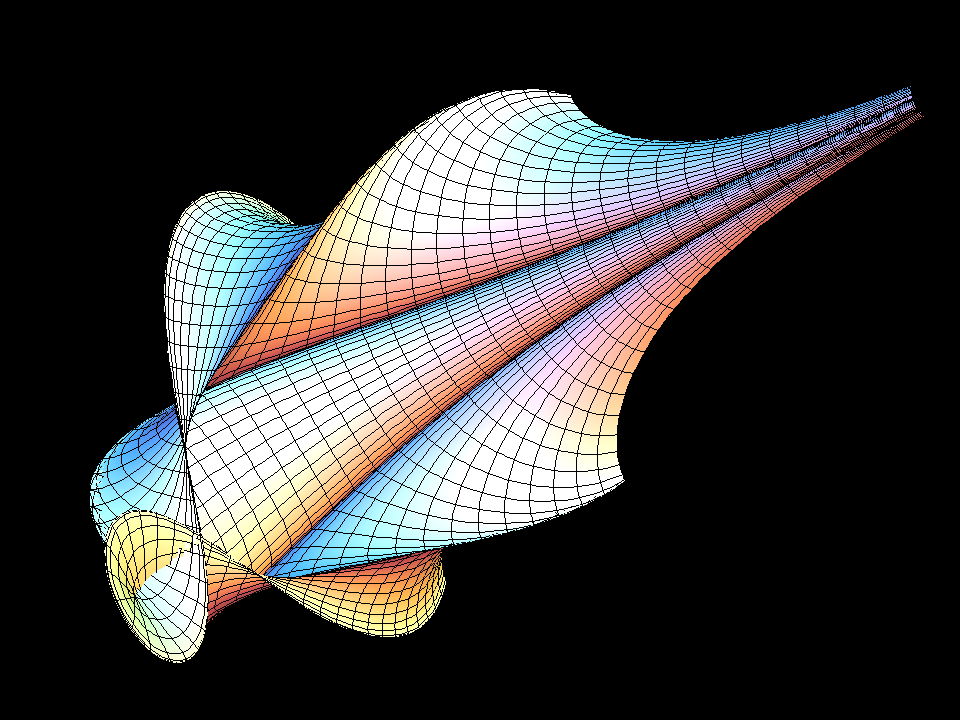
three-soliton morphS 001 — To reduce the selfintersections we only use -7 ≤ u ≤ 0. The constants change symmetric to 0.5, (b+c)/2 = 0.5: a = 0.5, 0.29 ≤ b ≤ 0.79, 0.71 ≥ c ≥ 0.21.

three-soliton wcomp-anagl — This anaglyph image shows how the computation procedes: at first one curvature line from “end” to “end” is computed, then the family of curvature lines orthogonal to the first one. The program proceeds not in equal sized steps but in steps of size cos(q/2) on one family and in steps of size sin(q/2) on the other family. The result is that the diagonals of the little paramter quadrilaterals all have the same(!) length: the diagonals look like a fisher net stretched over the surface. The sharp rims occur when sin(q/2) = 0 or cos(q/2) = 0: the curves stop there and proceed in the opposite direction.

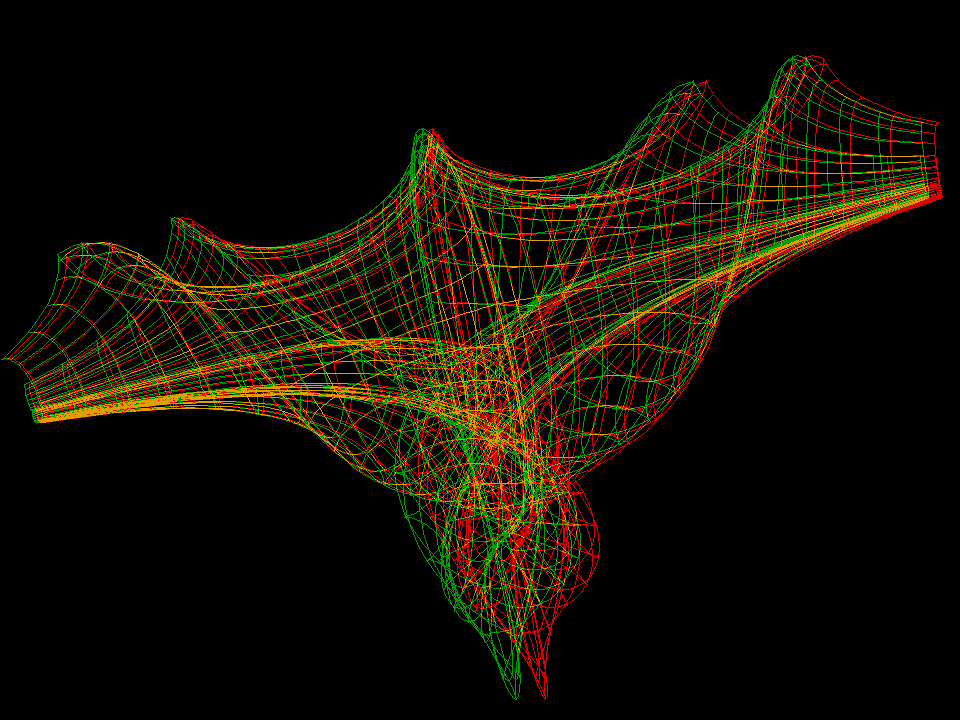
three-soliton wire-ana1 — The finished (anaglyph) wire frame image allows to check the statements underneath the previous image above.

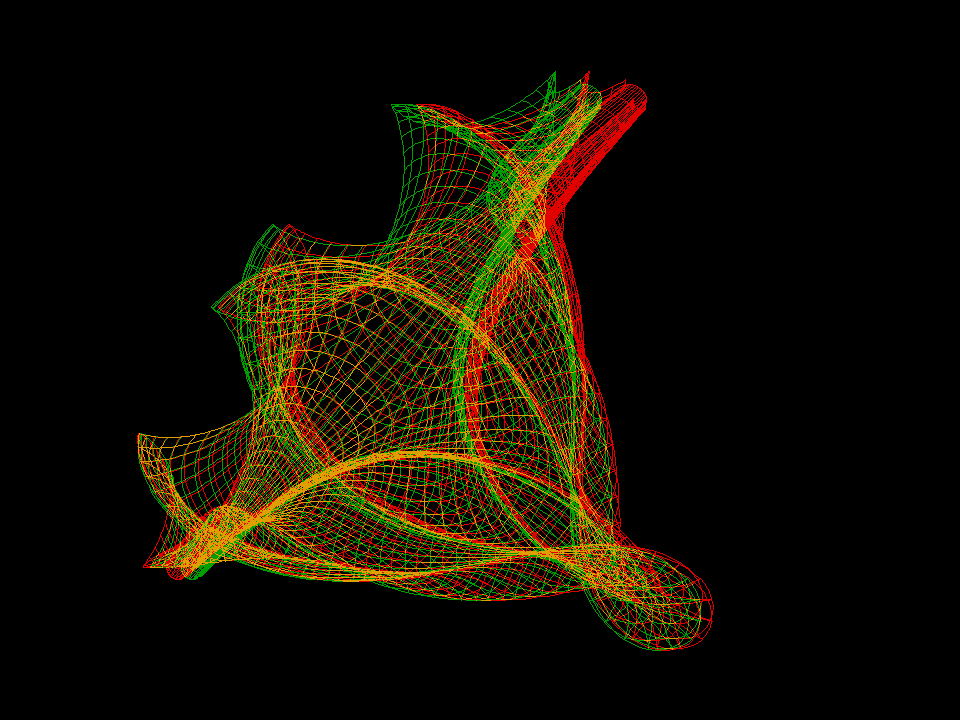
three-soliton wire-ana2 — Another wire frame image from a different direction.

Let us add that the pseudospherical surfaces bring together two beautiful mathematical constructions. On the one hand, a modern interpretation of a theorem of Bianchi allows to explicitly find a sequence of more and more complicated soliton solutions q(a,b, …; u,v) of the Sine-Gordon equation (Terng-Uhlenbeck). On the other hand, given such a solution, one can explicitly write down so called “first and second fundamental forms” to define a surface with K = -1. Before one has the parametrized surface (u,v) ⟶ F(u,v) in R^3, the first fundamental form allows to compute for a curve (u(t),v(t)) in the domain the length which the corresponding curve F(u(t),v(t)) on the surface would have. Similarly, the second fundamental form then gives all the curvature information for the curve on the surface, BEFORE one actually has the surface! length- and curvature-information for a space curve allow to write an ODE which then determines a space curve with these length- and curvature-data. These ODEs are solved for the first anaglyph picture above. Finally, if for each fixed v the would be surface curves u ⟶ F(u,v) have been computed, then one has without further computation the transversal curves v ⟶ F(u,v). Do they also satisfy their own ODEs? YES, because the function q (which we used to make first and second fundamental forms) is a solution of the Sine-Gordon equation! (In differential geometry one has, more generally, for this final compatibility the Gauss- and Codazzi equations, but our first and second fundamental forms are so special that the Gauss- and Codazzi equations reduce to the Sine-Gordon equation.)

Three-Soliton Surface

Related Surface