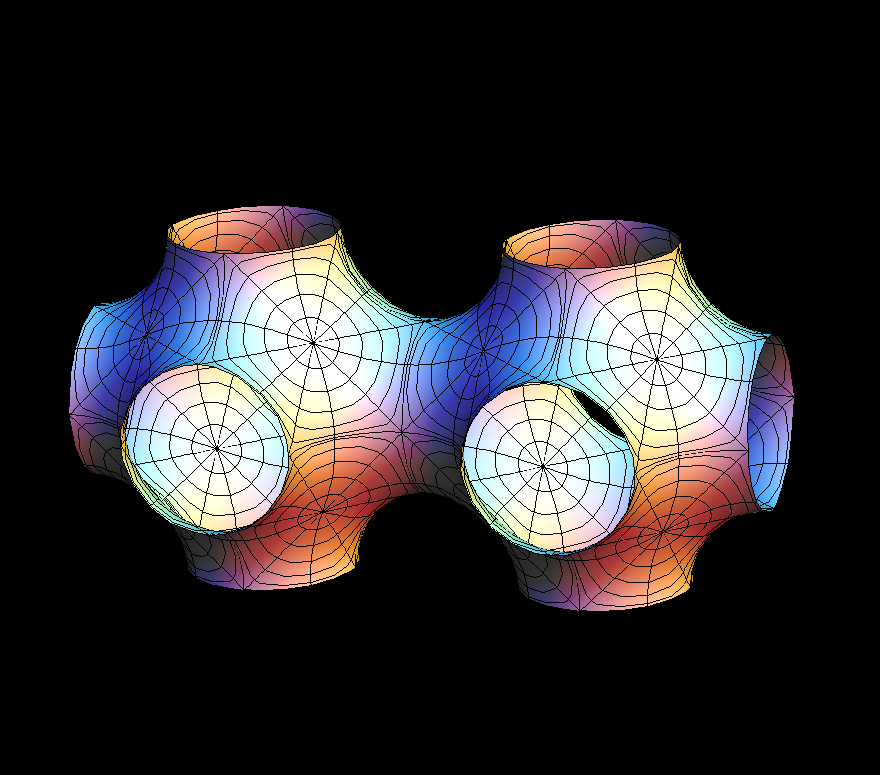

Imagine these surfaces built from pieces which sit in a “brick” and meet the brick's 6 faces in convex curves. Reflection in the planes of these curves extends the surface to a larger one. Eventually it fills R^3. It has translation symmetries in 3 directions, hence it is called “triply periodic”.
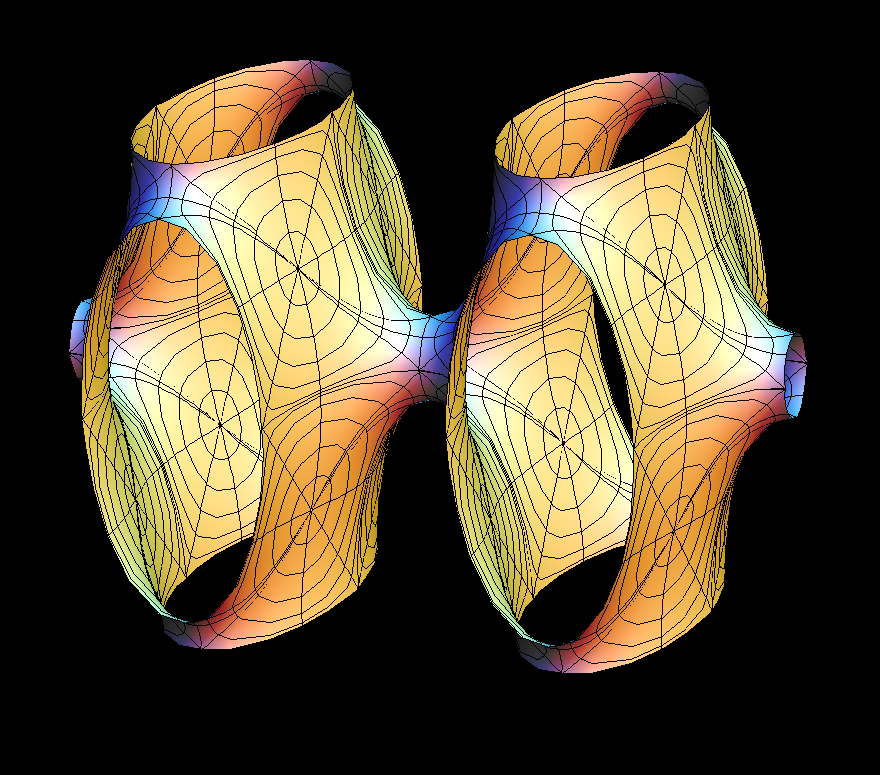
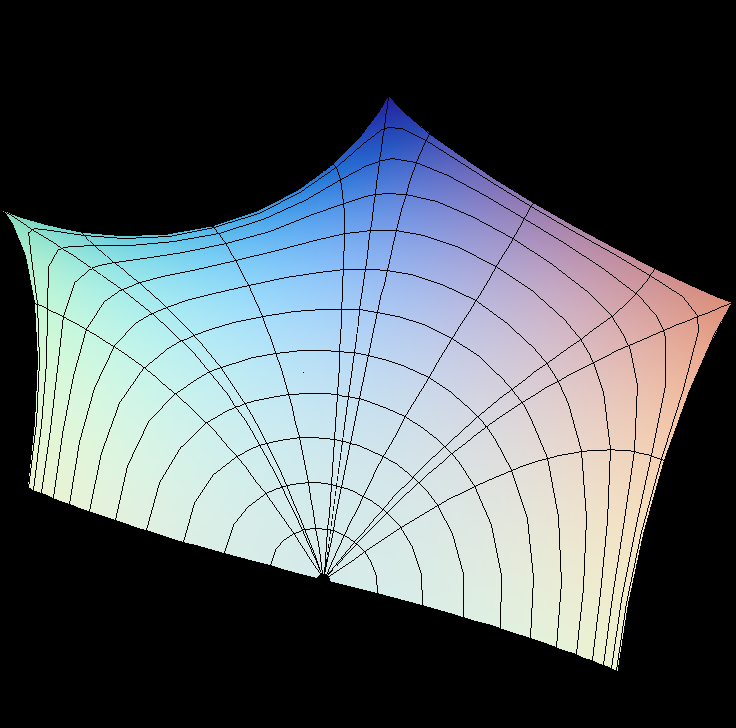
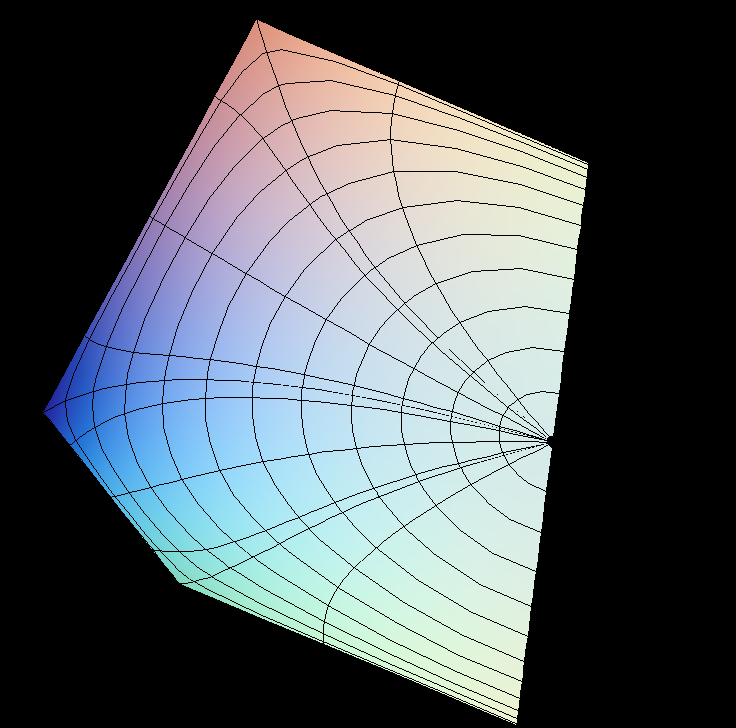
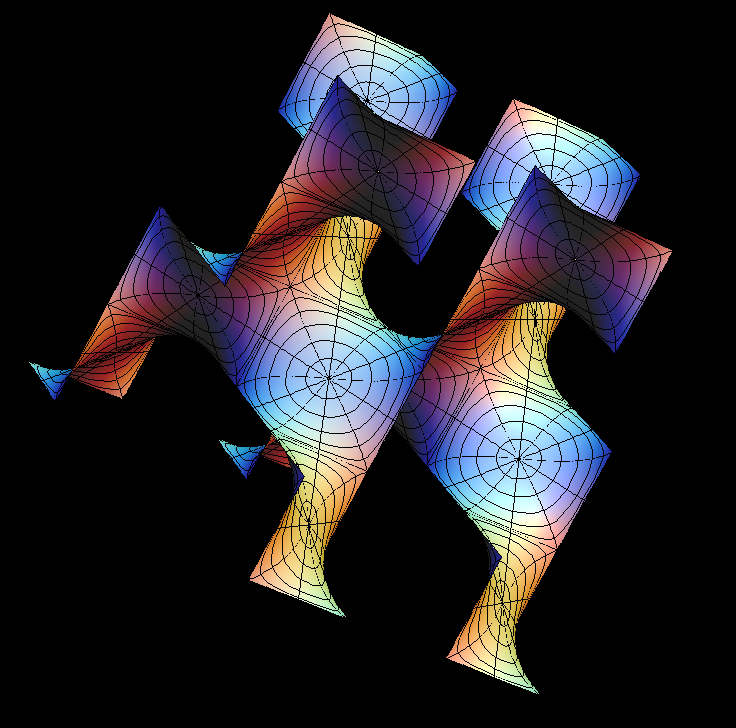
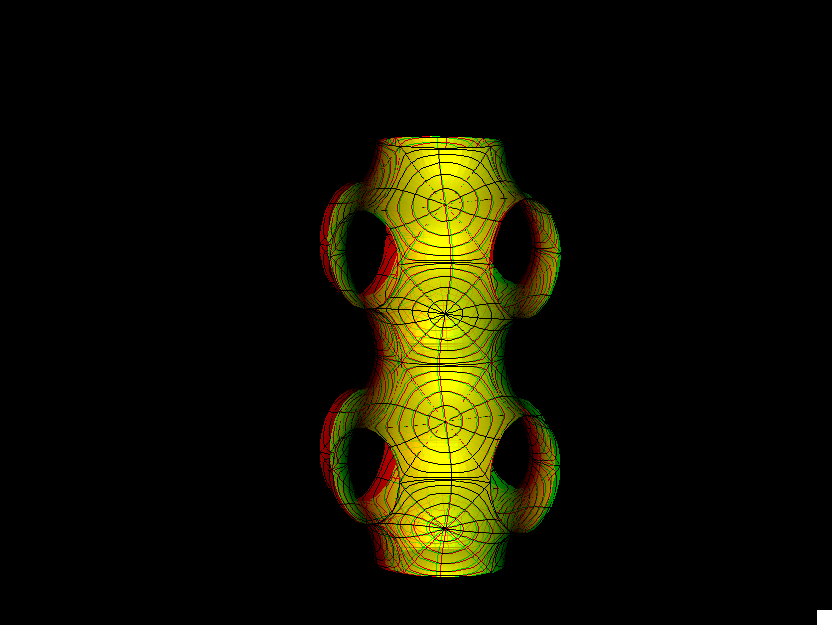
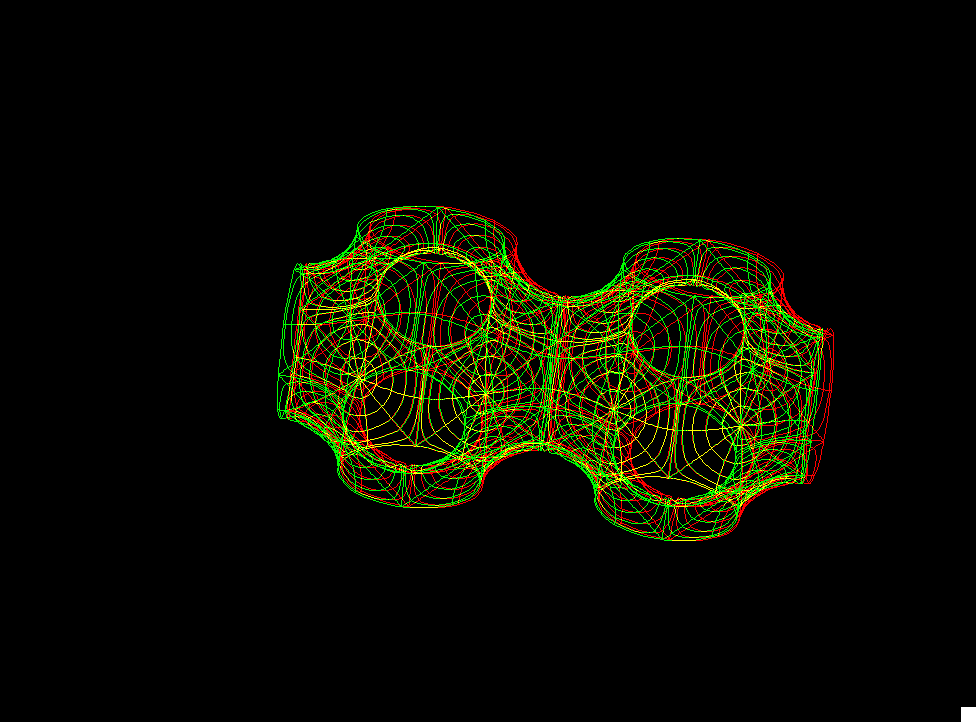
This is a 2-parameter family of triply periodic genus 3 surfaces. In each case the original surface and the conjugate surface are embedded. The most symmetric example (with a cubic lattice) which is obtained when cc = 0, dd = 0, was already constructed by H. A. Schwarz. When Alan Schoen found more triply periodic surfaces around 1970 he named the two surfaces which Schwarz found the P-surface (P for cubic primitive) and the D-surface (D for diamond). He also found a third embedded(!) surface in the associate family of these, the Gyroid (associate parameter 0.577 which is approx. 52 degrees). If dd=0 then a fundamental cell for the lattice is a prisma with square base, in the morphing cc changes the height of the prisma.
K. Grosse-Brauckmann, M. Wohlgemuth: The Gyroid is embedded and has constant mean curvature companions. To appear Calc. Var. 1996
For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see either [KWH], or pages 192--217 of [DHKW].