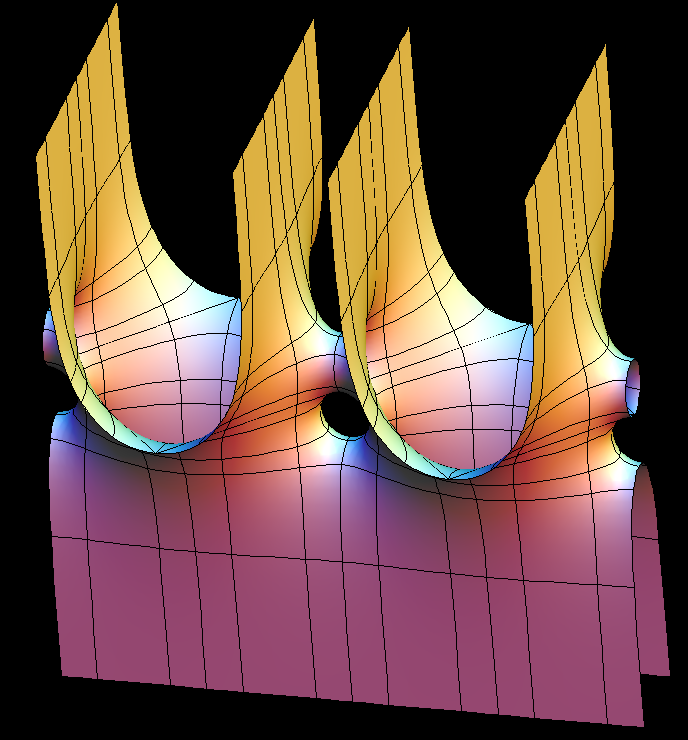
Scherk with Handle

scherk with handle
Scherk with Handle
scherk handle asso graph 001
“scherk handle asso graph 001”
The conjugate fundamental piece is rotated so that its boundary projects one-to-one to a straight strip. This implies that there is only one Plateau solution and this solution is a graph over the strip. Romain Krust concluded from this (and told me) that all surfaces of the associate family are graphs (over complicated domains) and graphs are always embedded surfaces.
scherk handle associate 001
“scherk_handle_associate_001”
Associate family morph of the fundamental piece of scherk_with_handle. The conjugate piece is bounded by two straight segments and 4 half lines. This implies that the original piece is bounded by planar symmetry lines (the complete surface is reflection symmetric with respect to their planes).
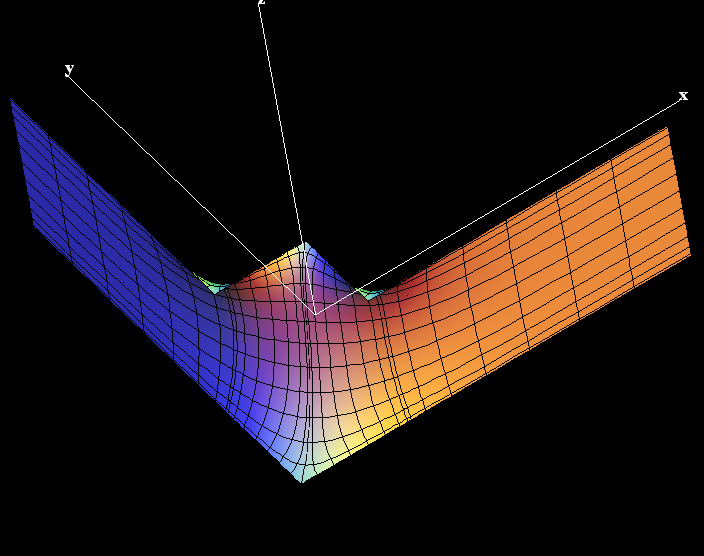
scherk with handle conj 001
scherk with handle conjugate
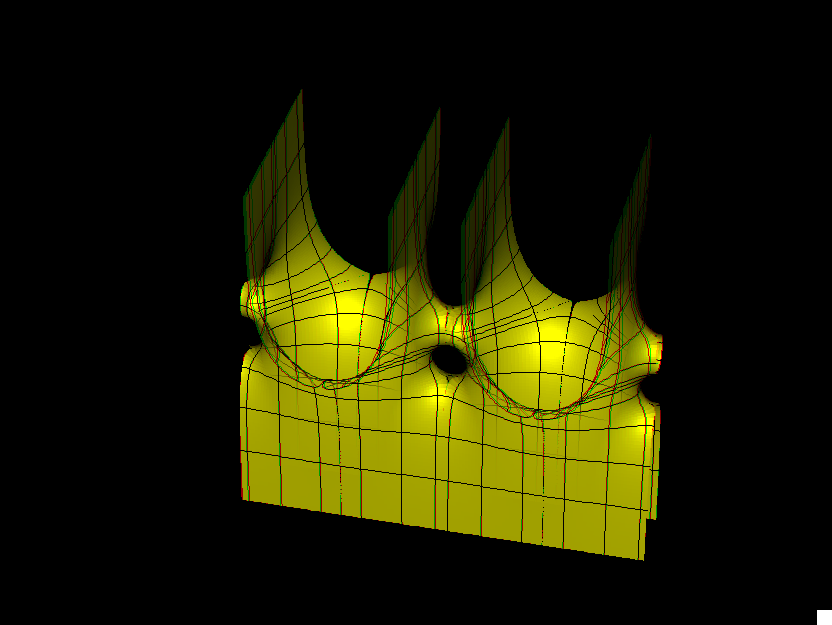
scherk w handle st
scherk w handle st
scherk w handle sw
scherk w handle sw

About the Scherk Surface with Handle

This surface is a genus one version of Scherk's doubly-periodic surface. Existence and embeddedness is proved in [KWH], and our formulas are from there.

The conjugate fundamental domain is bounded by straight lines. This piece can be rotated to be a graph over a convex domain, and in this position the original piece is also a graph. For this we suggest the associate family morphing.

The surface has a period problem, because the position of the punctures is not determined on the square Torus by qualitative considerations. We suggest the (joint) position of the punctures as morphing parameter (ee), again to illustrate the use of intermediate value arguments for killing periods.

For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see either [KWH], or pages 192--217 of [DHKW].

Get red/blue stereo glasses from amazon

Scherk_w_Handle.pdf