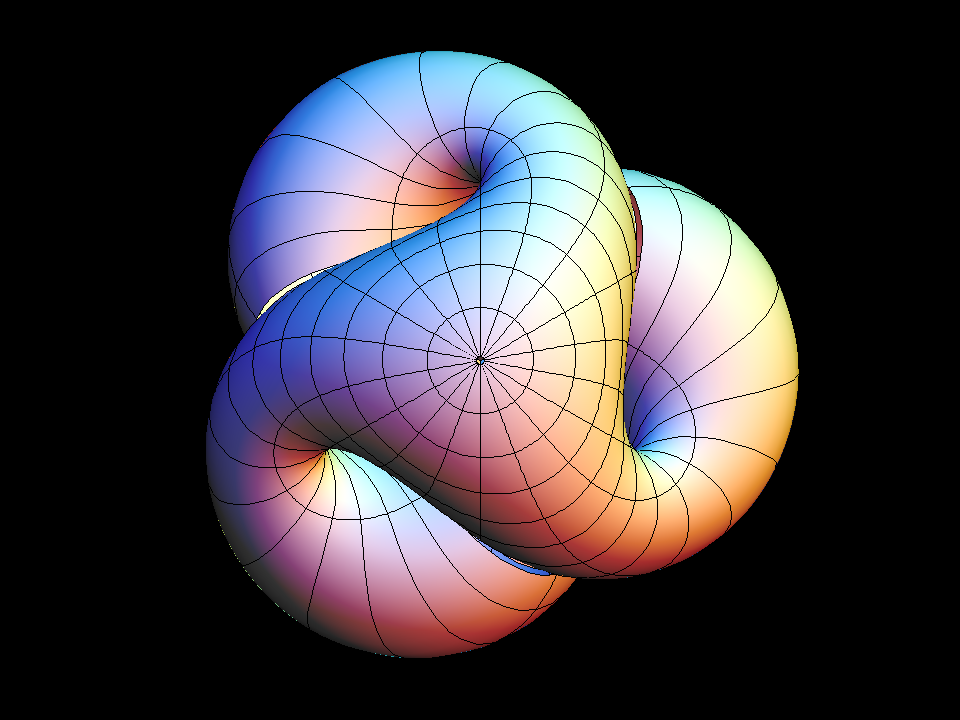
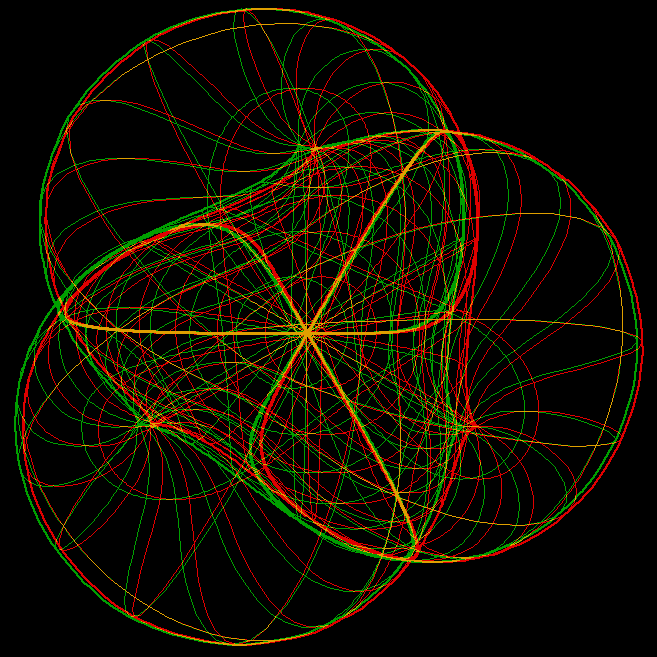
Boys Surface (After Bryant-Kusner)
Hermann Karcher
See the moebius strip first.
The non-orientable surfaces are "one-sided",
and this concept can best be understood if one starts from a Moebius Strip.
The Klein Bottle is easier to visualize than the Boys surface. Each meridian
of the Boy surface is the center line of a narrow Moebius band, for example
use "Set u,v ranges" to set umin = - 0.998, vmin = 6.1.
The "equator" of the Boys Surface is a different Moebius band. It has three
half-twists instead of one. The standard morph begins with this Moebius band
and widens it until the Boys Surface is complete:
aa = 0.5,\ vmin = 0, vmax = 2\pi, umax = 1,
0.9 > umin > 0.002 .
The Boys Surface is really a family of surfaces. Boys, in his dissertation
under Hilbert, constructed an immersion of the projective plane. Being
non-orientable implies that no embedding is possible. Boys Surface has
besides its self-intersection curves only one more serious singularity,
namely a triple-point. His construction was topological.
Apery found algebraically embedded Boys Surfaces. They carry
one-parameter families of ellipses.
The Bryant-Kusner Boys surfaces are obtained by an inversion from
a minimal surface in R^3. The minimal surface is an immersion
of S^2 - 6 points such that antipodal points have the same image
in R^3. The six punctures are three antipodal pairs, and the
minimal surface has so called "planar ends" at these punctures.
In this context it is important that the puncture in the inversion
of a planar end can be smoothly closed by adding a point. The
closing of the three pairs of antipodal ends thus gives a triple
point on the surface obtained by inversion. Explicitly:
Let M(z) = Re( a(z) V(z) ) + (0,0,1/2)
where a(z) = 1/(z^3 - z^{-3} + sqrt(5) ) and
V(z) = ( i ( z^2 - z^(-2) ) , z^2 + z^(-2) , (2 i/3) ( z^3 + z^(-3) ) )
Then Boys(z) is obtained by inverting M(z) in the unit sphere:
Boys(z) = M(z)/ || M(z) ||^2