Symmetric 4-noid

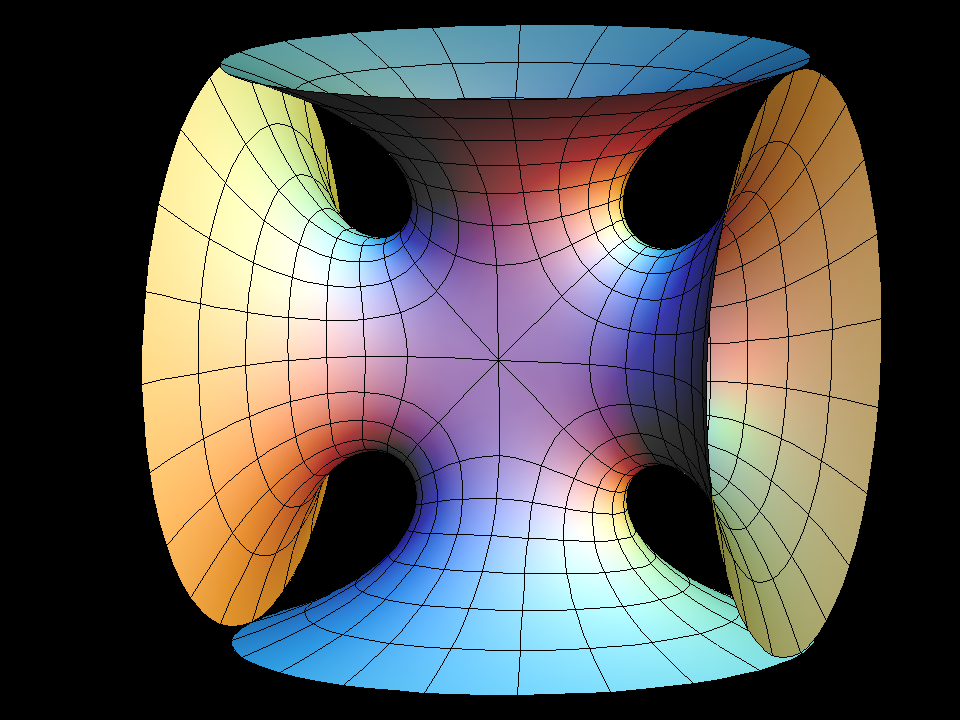
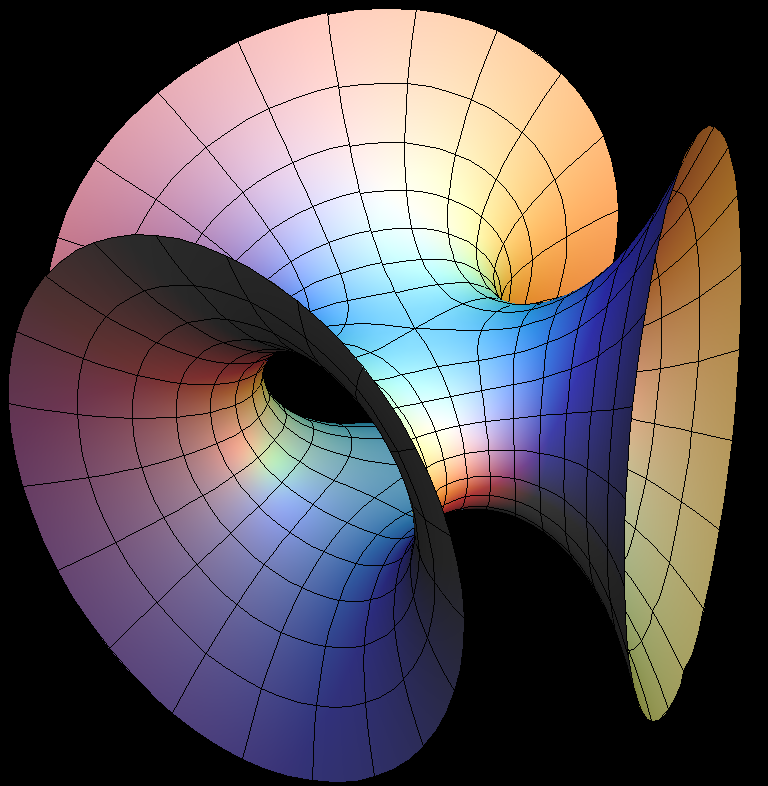
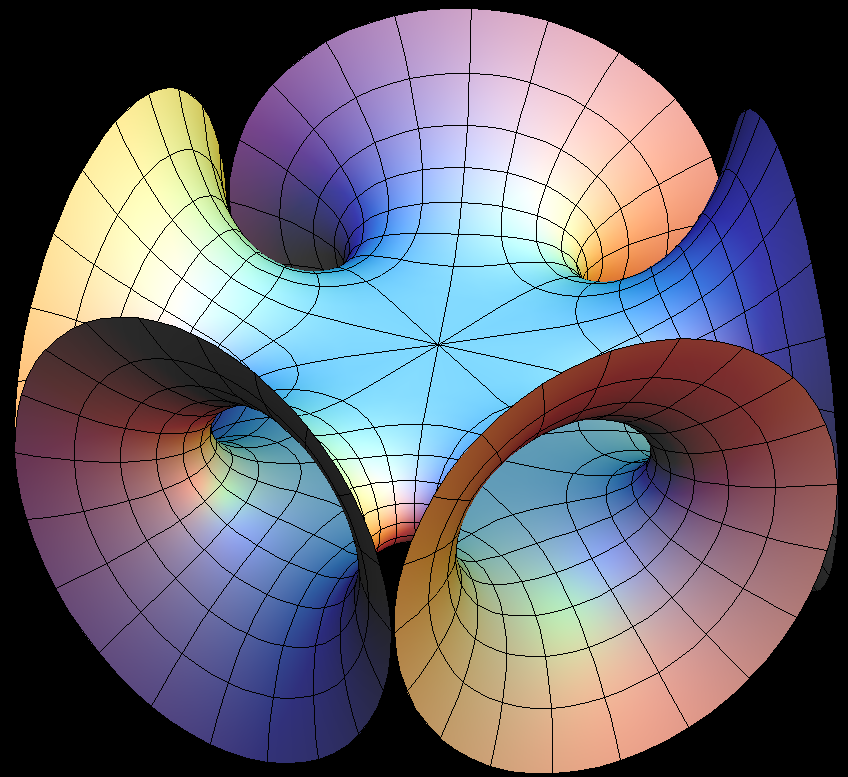
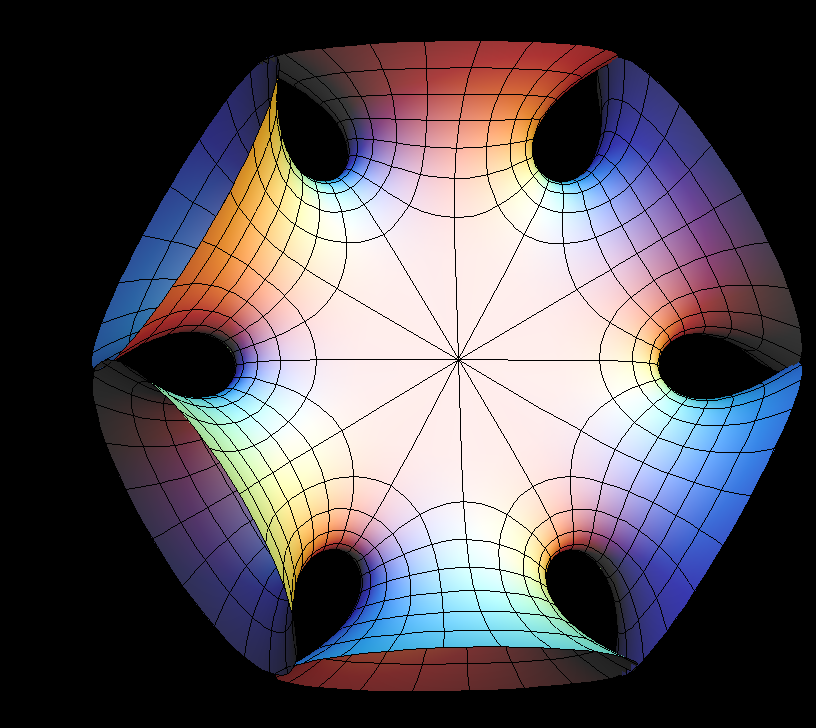
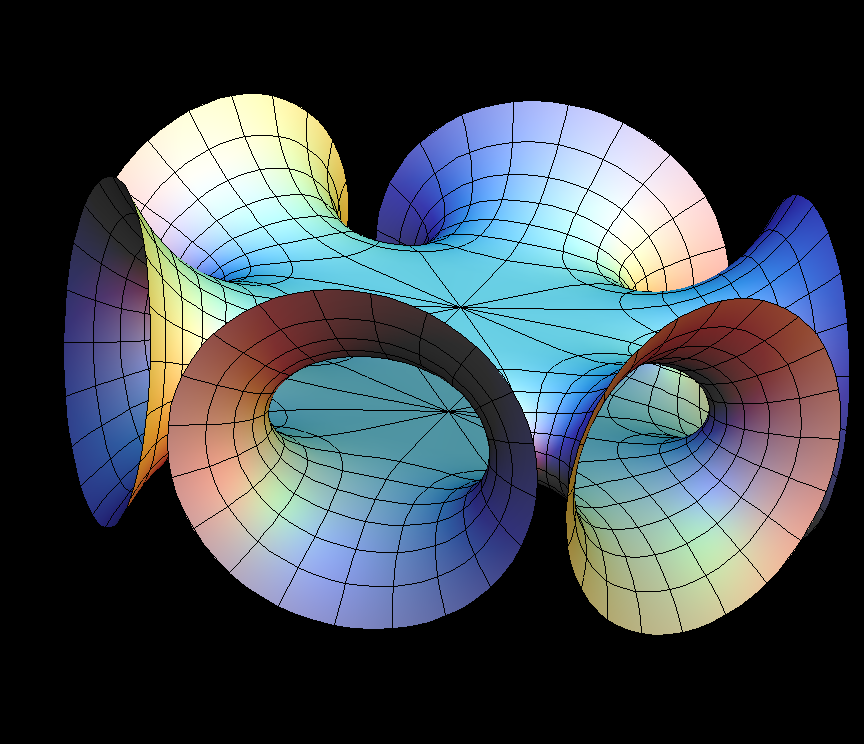
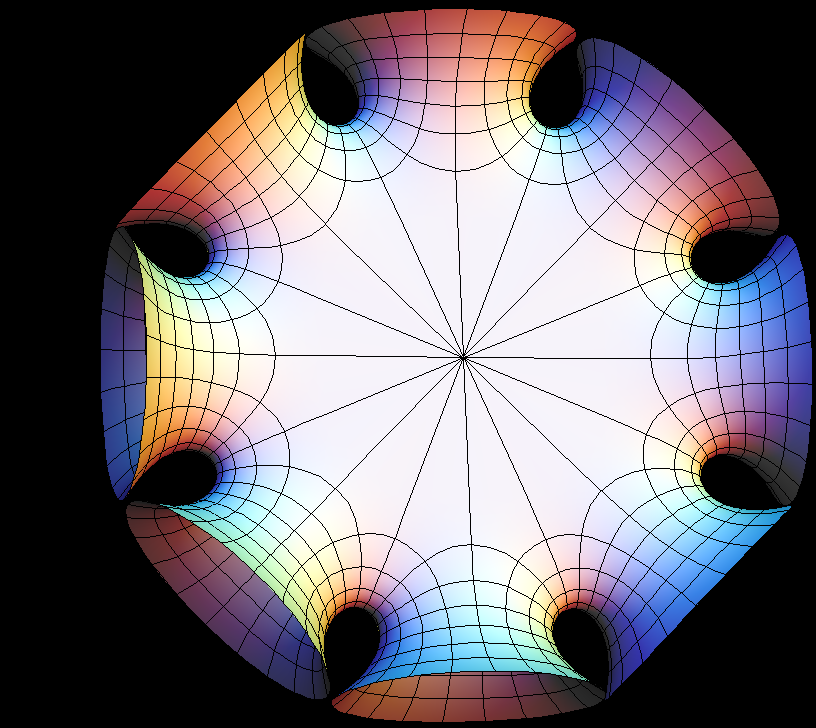
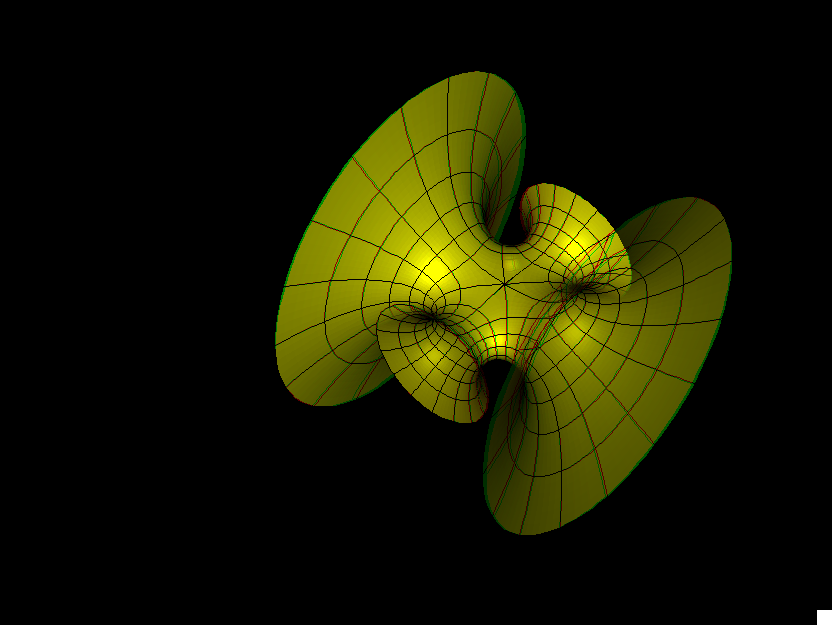
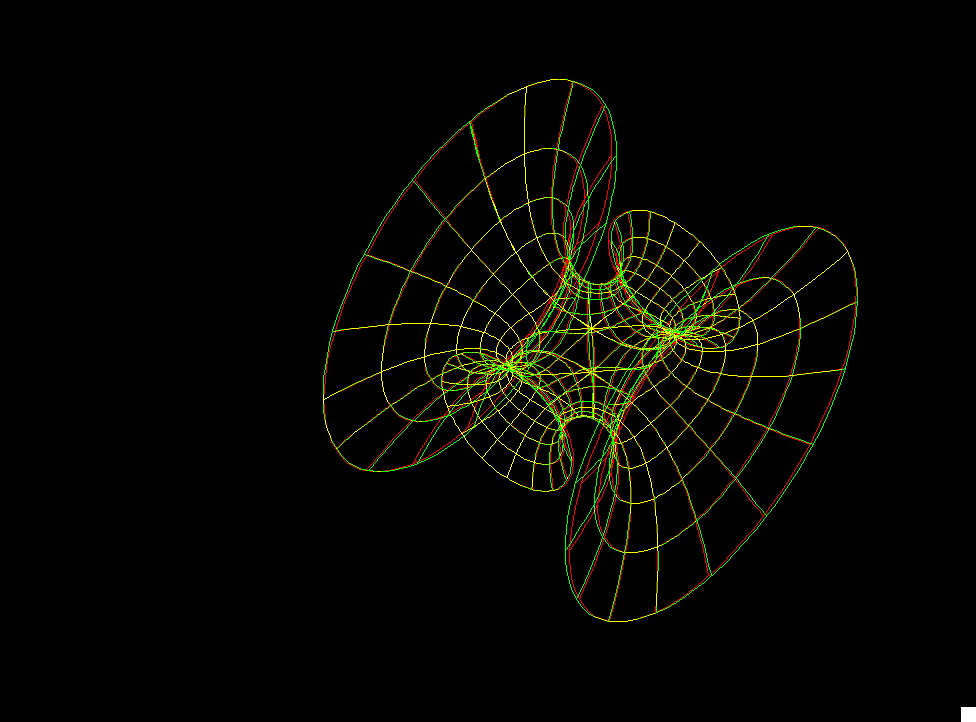
The Symmetric 4-noid and Skew 4-noid are parametrized by 4-punctured spheres; we use lines which extend polar coordinates around the punctures. Formulas are from [K2].

The intersection of the two families is the 4-noid from the Jorge-Meeks family of k-noids. These k-noids are the first finite total curvature immersions where the Weierstrass data were manufactured to fit a previously conceived qualitative global picture of the surfaces.

We suggest morphing the relative size of the opposite pairs of catenoid ends in the symmetric case and the angle between the catenoid ends in the skew case. The skew surface family goes from the Jorge-Meeks 4-noid to surfaces which look like two catenoids joined by a handle. This convinced David Hoffman that the idea of adding handles might be promising.

Formulas are taken from:

• Construction of Minimal Surfaces, H Karcher , in “Surveys in Geometry”, Univ. of Tokyo, 1989, and Lecture Notes No. 12, SFB 256, Bonn, 1989, pp. 1 — 96.

For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see:

• [KWH] H. Karcher, F. Wei, and D. Hoffman, The genus one helicoid, and the minimal surfaces that led to its discovery, in “Global Analysis in Modern Mathematics, A Symposium in Honor of Richard Palais' Sixtieth Birthday”, K. Uhlenbeck Editor, Publish or Perish Press, 1993
• [DHKW] U. Dierkes, S. Hildebrand, A. Kuster, and O. Wohlrab, Minimal Surfaces I, Grundlehren der math. Wiss. v. 295 Springer-Verlag, 1991