Riemann's Surface

riemann morph 001

The Gauss maps of these famous surfaces are the similarly famous Weierstrass p-functions on rectangular tori. [see Elliptic Function: JE]

Compare the image with the image of the Lopez-Ros No-Go Theorem [see Lopez-Ros-No-Go surface]

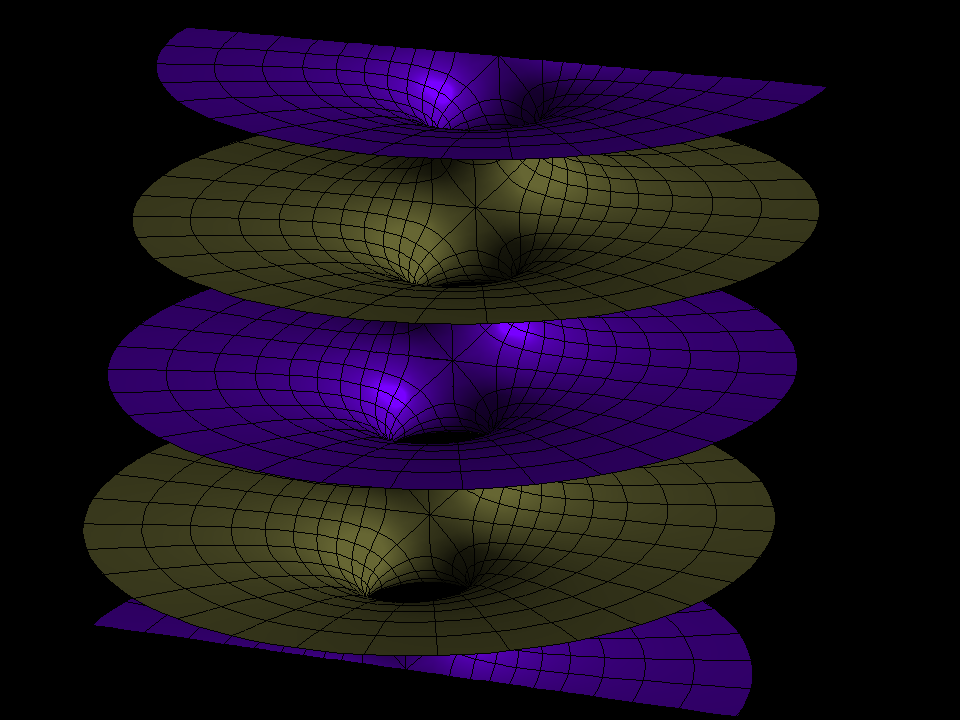
rieman twosided
The coloration of this image emphasizes the two sides of this surface. The translational symmetries are therefore not from one level to the next, but from one level to two levels up or down. These surfaces also have a less obvious symmetry: Observe the straight lines on each level (between the “handle up” and the “tunnel down”). The parallel line in the middle between two neighboring ones of the mentioned straight lines intersects the surface orthogonally and 180 degree rotation around this normal line maps the surface to itsself.
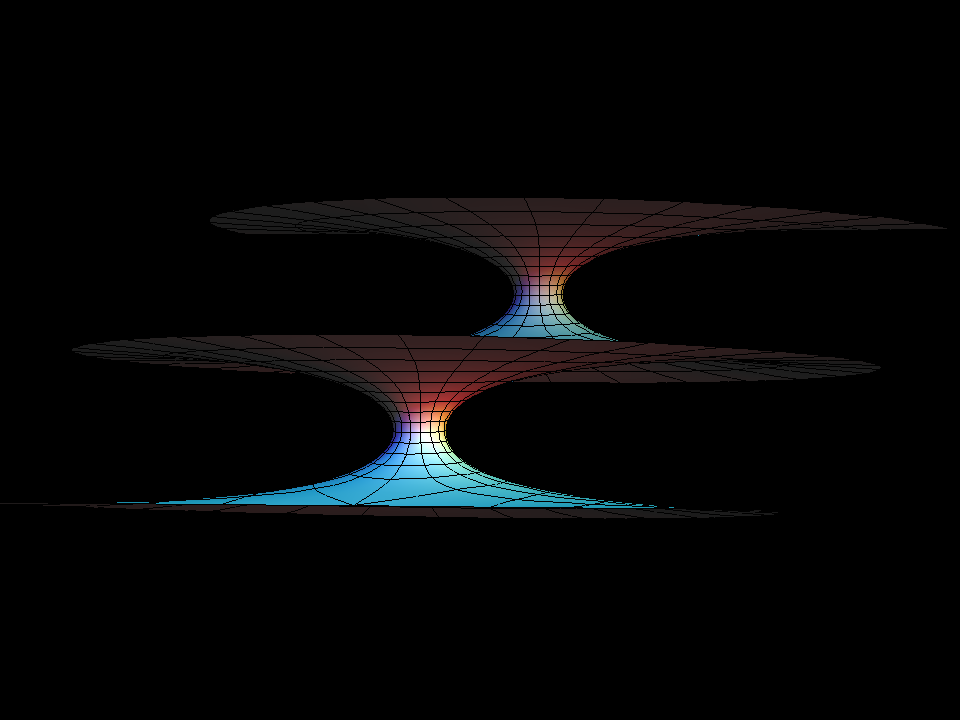
riemann associate 001
The Catenoid-like handles on one end of the associate-family-animation are deformed to Helicoid-Catenoid helicoid like portions on the conjugate surface, see both sides of the rather squeezed handle of the conjugate surface.
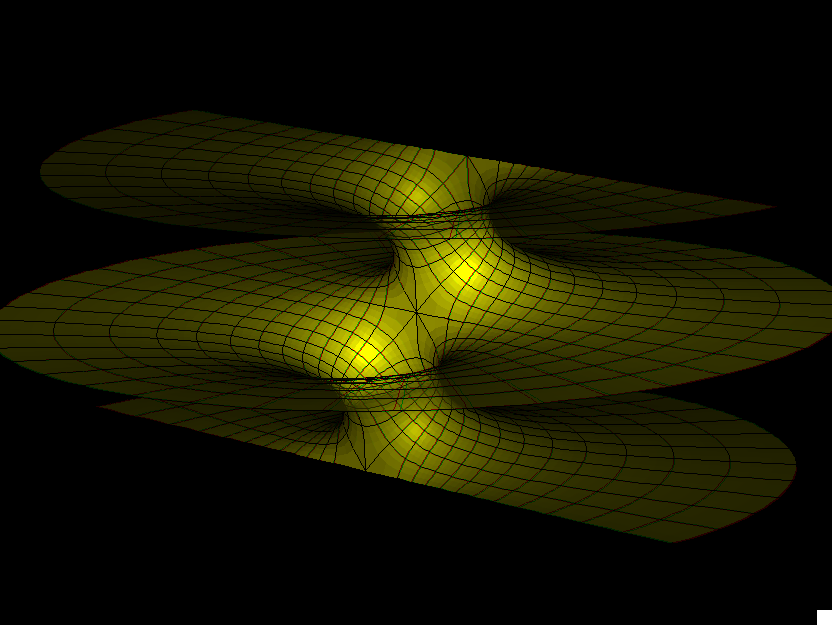
riemann st
riemann st
riemann sw
riemann sw

About Riemann's Minimal Surfaces

H. Karcher

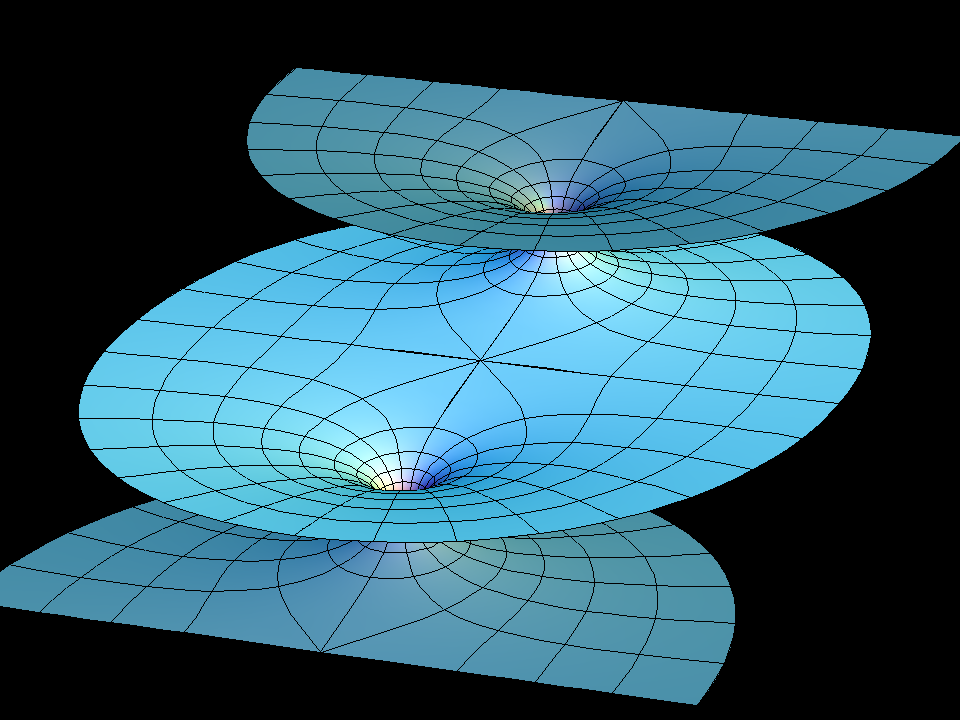
This is the family of singly-periodic embedded minimal surfaces found by Riemann. They are parametrized (aa) by rectangular tori. The Gauss map is the Weierstrass pe function additively normalized to have a double zero at the branch point diagonally opposite the double pole and multiplicatively normalized to have the values plus or minus i at the four midpoints (on the Torus) between the zero and the pole. The minimal surface has rotational symmetries around the corresponding normals. This symmetry kills the horizontal periods. The surface is parametrized by the range of the Gauss map with polar coordinates around the punctures. The surfaces look like families of parallel planes with one handle between adjacent planes. The associate family morphing joins two such embedded surfaces - they are congruent for the square Torus. The standard morphing (aa) changes the branch values of the Gauss map, i.e. the tilt of the normal at the flat points (K=0).

For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see either [KWH], or pages 192--217 of [DHKW].

riemann.pdf