
About the Lopez-Ros No-Go Theorem
The theorem of Lopez-Ros [LR] says that a complete, finite total curvature, minimal embedding of a punctured sphere is either a catenoid or a plane.
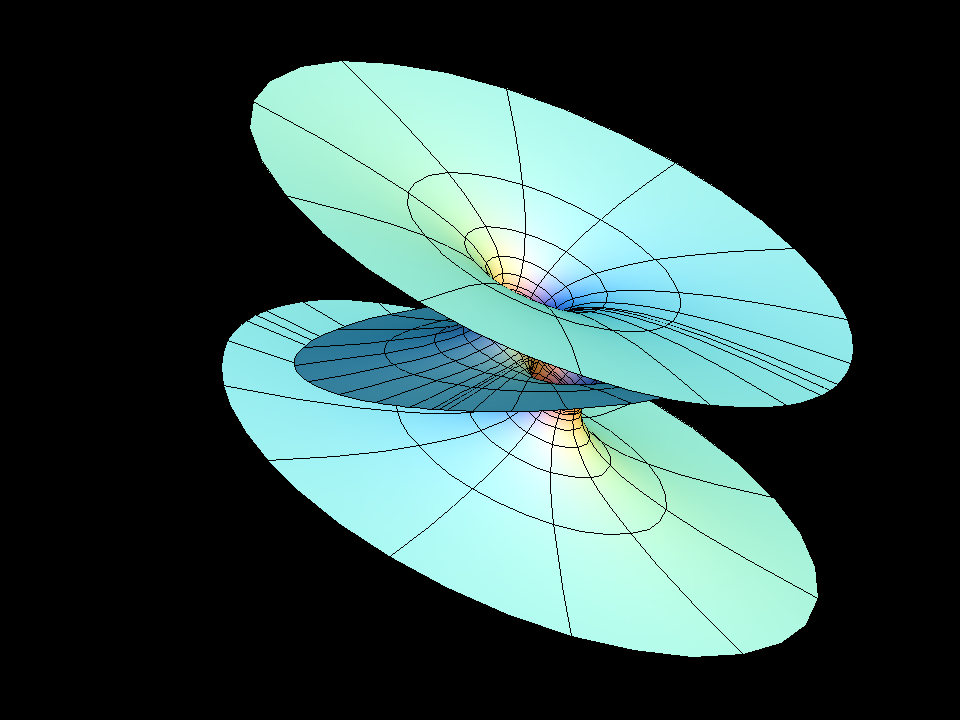
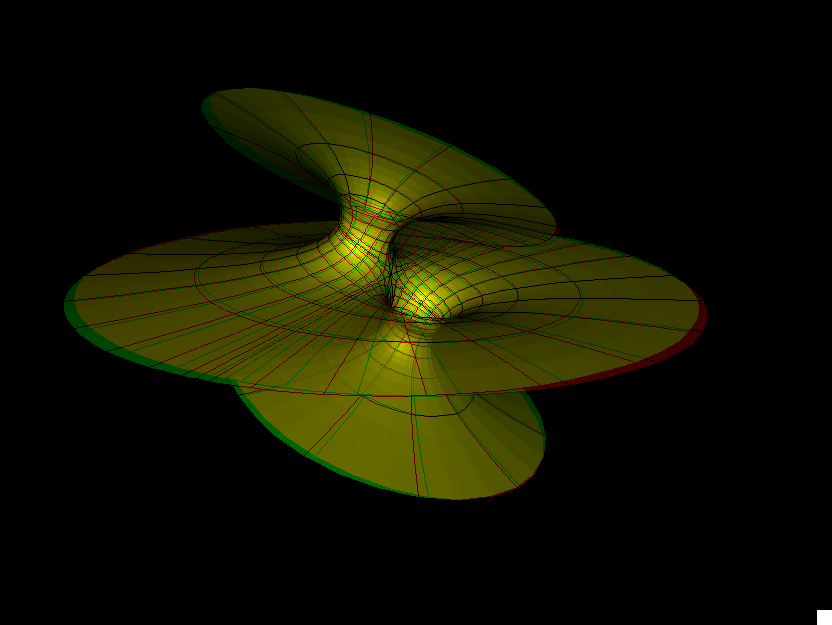
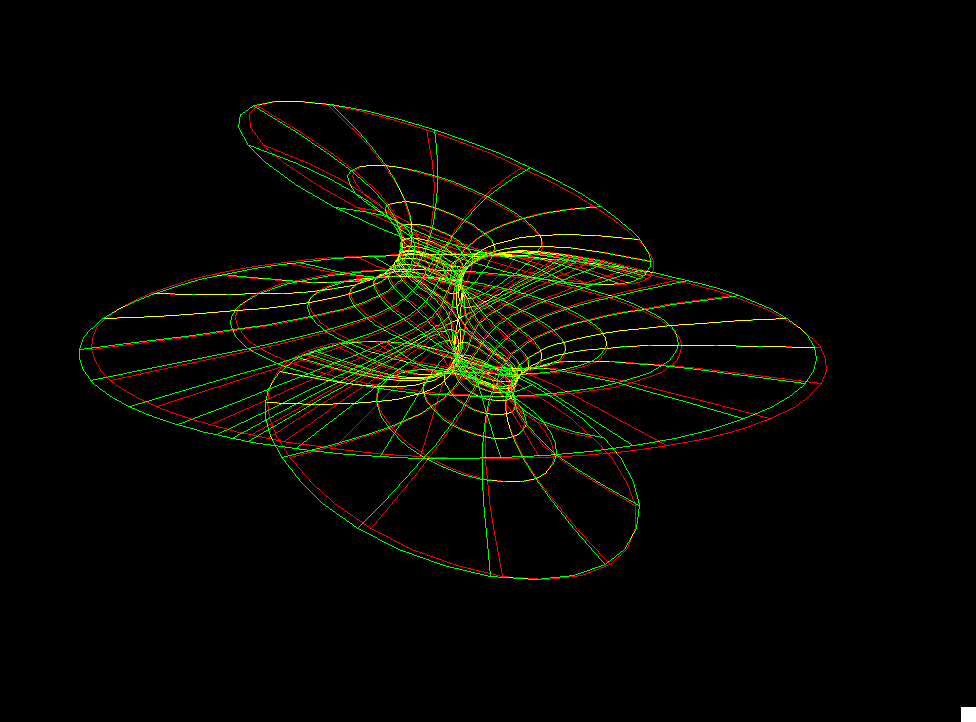
Our example is parametrized by a 3-punctured sphere, and its Gauss map is Gauss(z) = cc(z-1)(z+1). Parameter lines on the sphere extend polar coordinates around the punctures at z=+ee, z=-ee, z= ∞.
A necessary condition for embeddedness is parallel normals at infinity, i.e., ee=1. In this case the period cannot be closed. If ee<>1, then cc can be chosen to close the period, but then the catenoid ends are tilted so that they intersect the third (planar) end. -- For each ee<>1 we set cc0 to the value which closes the period; one can therefore see in the morphing how cc is used to close the period.
For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see either [KWH], or pages 192--217 of [DHKW].