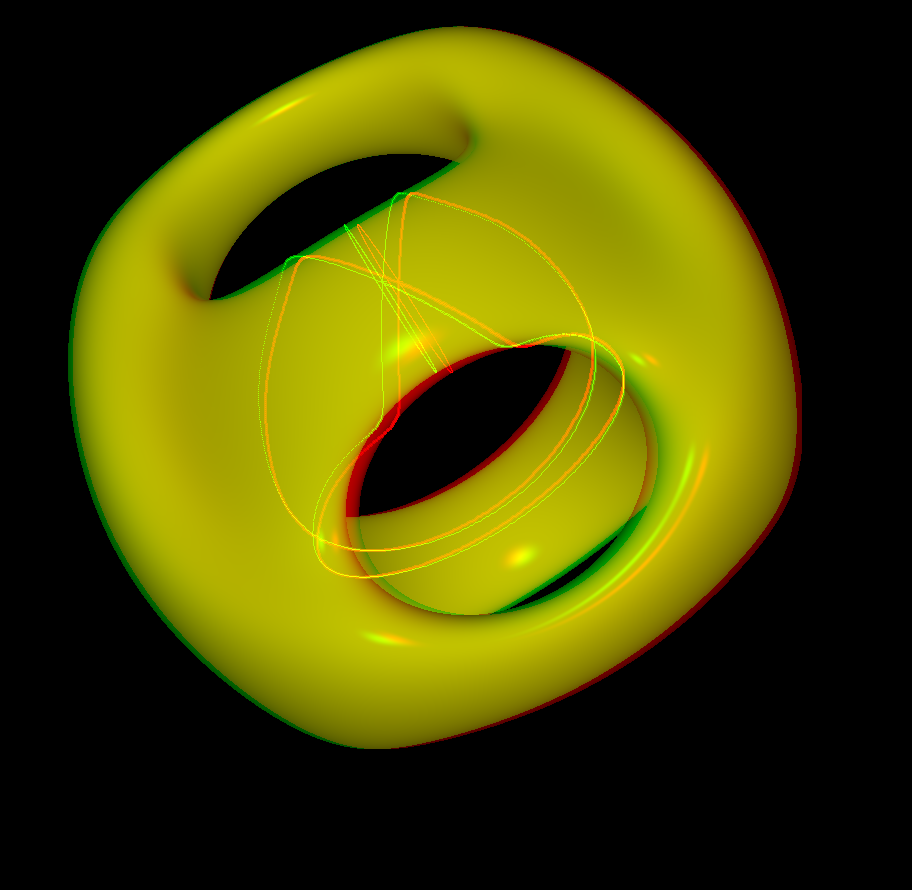
People have played with explicitly parametrized surfaces to produce shapes like the Snailshell or many others. One does not get closed surfaces of higher genus that way. Implicitly defined closed surfaces are easily obtained with high genus. This animation is one of the simplest examples: multiply two functions which each have an ellipse as minimum set and vary the distance of the two ellipses. — Join of 2 Tori and Bretzel5 Implicit Surface are similar examples.
The Pilz surface is a algebraic surface given by
f(x,y,z) := ((x^2 + y^2 - 1)^2 + (z -0.5)^2)^2) *
( (y^2/aa^2 + (z + hh)^2 -1)^2 +x^2) -
ff * (1 + bb*(0*x^2 + 0*y^2 + (z-0.5)^2))
default: ff = 0.28 hh = 0.03