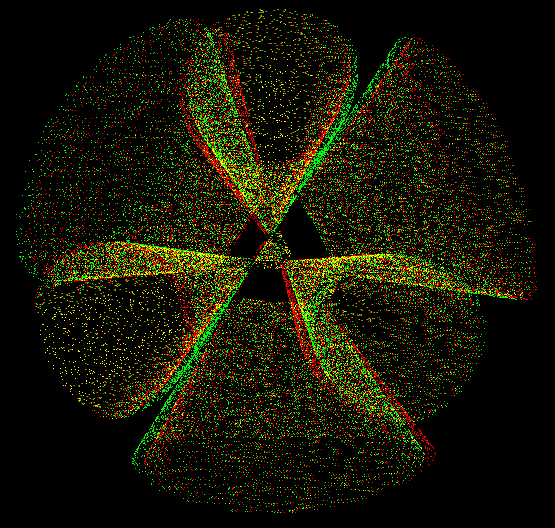
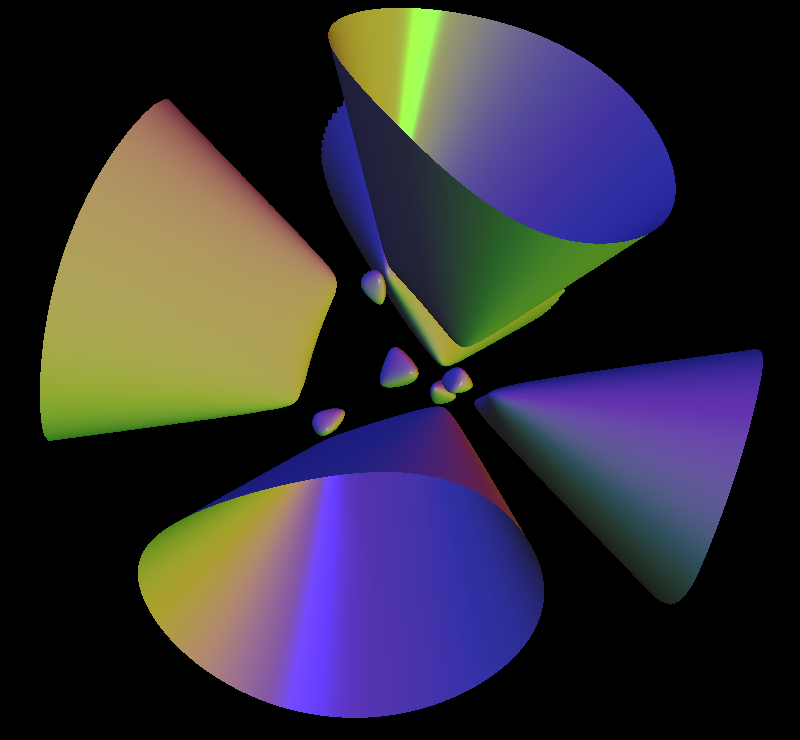
A Kummer surface is any one of a one parameter family of algebraic surfaces defined by the polynomial equation of degree four:
(x^2 + y^2 + z^2 - aa^2)^2 - lambda*p*q*r*s = 0. Here aa is any real number. lambda = (3*aa^2 - 1.0)/(3 - aa^2) p = 1 - z - sqrt(2)*x q = 1 - z + sqrt(2)*x r = 1 + z + sqrt(2)*y s = 1 + z - sqrt(2)*y
The family was described originally by Ernst Eduard Kummer In 1864.
A Kummer surface has sixteen double points, the maximum possible for a surface of degree four in three-dimensional space. For the default case aa = 1.3, all these double points are real and they appear in the visualization as the vertices of five tetrahedra.
p(x,y,z) = c for c = -0.1, -0.05, 0, 0.05, 0.1.