The Gyroid and the Lidinoid are the only known triply periodic embedded minimal surfaces which are NOT cut by straight symmetry lines and/or planar symmetry curves into simple pieces.
Gyroid is discovered by Alan Schoen.
The Gyroid has been intensely studied by material scientists. It has been observed as the interface between two different polymeres.

The Gyroid is in the associate family between the Schwarz P-surface and its conjugate, the Schwarz D-surface - here the case with cubical symmetry.
Both the P- and the D-surface have reflection symmetries in planes and 180 degree rotation symmetries about lines on the surface. These symmetries are not present for the other surfaces of the associate family, but, amazingly, many other symmetries persist for all surfaces of the associate family.
All the polar centers visible on the surfaces are centers of point-reflection symmetries. 120 degree rotations around the normals at these points are further surface symmetries. !80 degree rotations around the normals at the other singular points of our paramter grid are the third group of symmetries which persist for all members of the associate family.
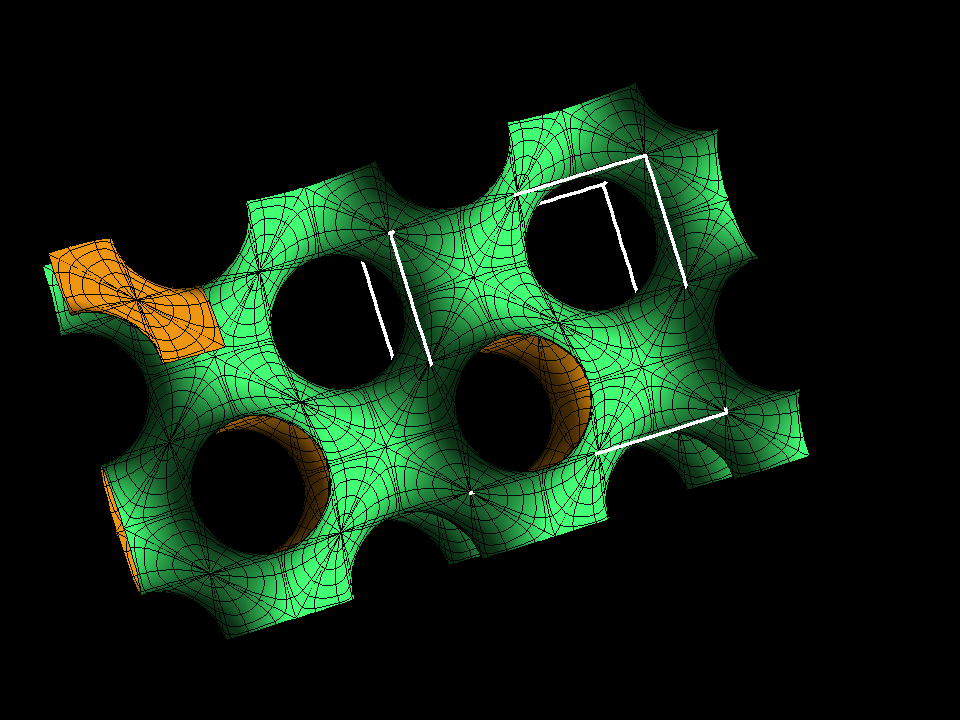
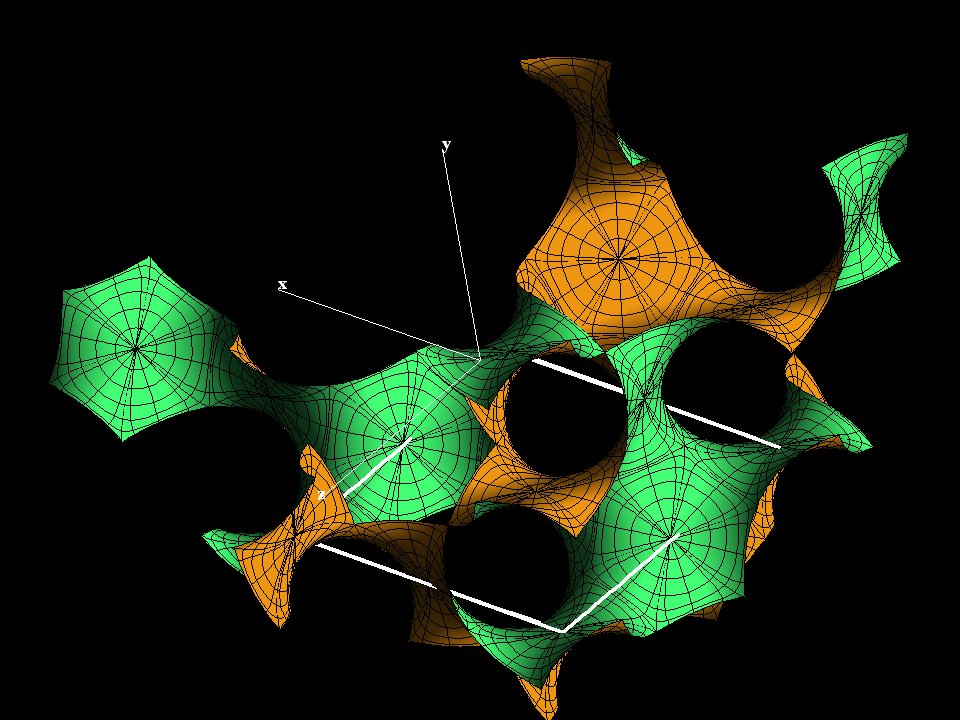
We group the polar centers of the P-surface in four families, where the surface normals in each family are parallel to one of the space diagonals of the lattice cube (indicated in white). All surfaces of the associate family are covered by similar four families of parallel polar “disks” with the described symmetries (these disks have a hexagon boundary with 90 degree angles).
To see what is special for the Gyroid we have to look at the translation symmetries. The composition of any two point-reflection symmetries is a translation symmetry. These translations fit together to form a lattice for the P- and D-surfaces and for the Gyroid - for the other associate family surfaces there are too many symmetries.
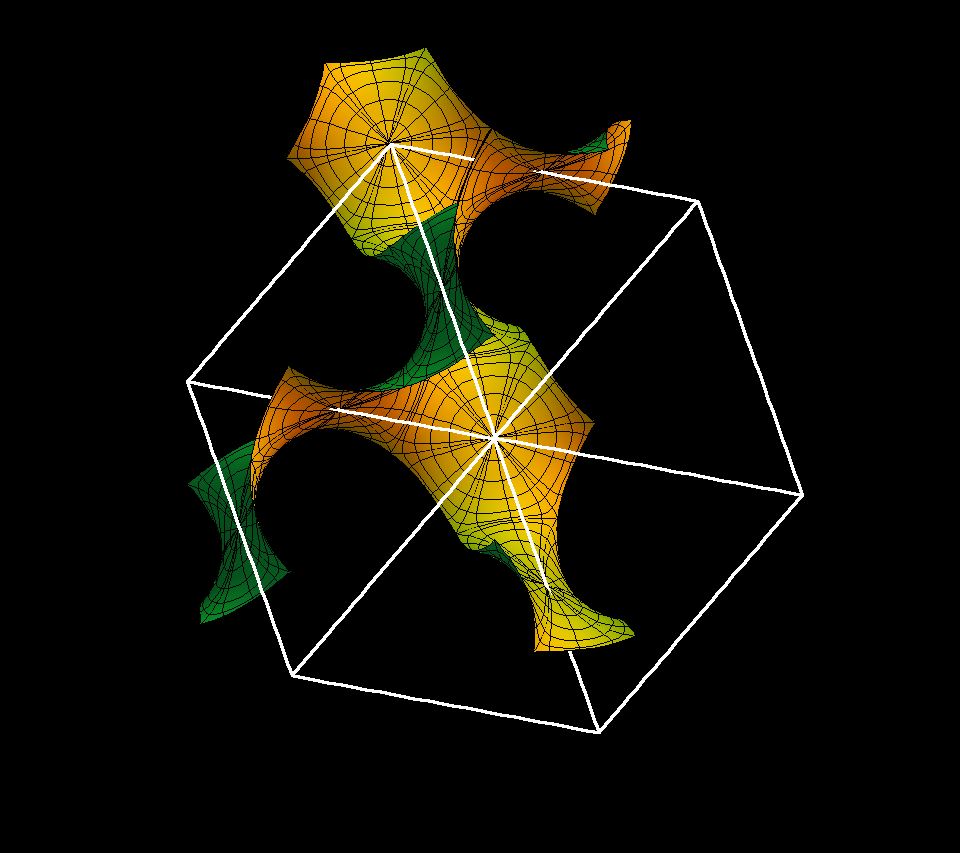
The Gyroid has more symmetries than any of its lattices. The cubical fundamental cell of the P-surface deforms in our deformation to a cell for the Gyroid. This cell has all edgelengths the same. The shorter face diagonals are a bit longer than the edges and they are parallel to the original x-, y-, z-axes. The edges and the short space diagonal of this cell are parallel to the space diaonals of the original cube and they are parallel to the surface normals at the hexagon centers.
This same animation can be viewed in anaglyph below.

This image clearly shows the 3-fold symmetry of the Gyroid. Around the central hexagon one can see three triples of parallel hexagons (with alternating orientation). The other 120 degree symmetries are less clear.
In this animation the fundamental cell is rotated to look like a regular hexagon. This is the same position as in the previous image. The animation adds more tiles, which may help to imagine the distances vertical to the screen.
This rotation animation of the Gyroid passes through several special positions: In the first image four edges of the cell are orthogonal to the screen. In the last image two short face diagonals are orthogonal to the screen. Roughly in the middle the short space diagonal is orthogonal to the screen.

This anaglyph animation shows the same associate family deformation from the Schwarz P-surface to the Gyroid as the first sequence above. If one has red-green-glasses then the complicated spatial relations of the hexagon tiles of the surface can more clearly be seen.