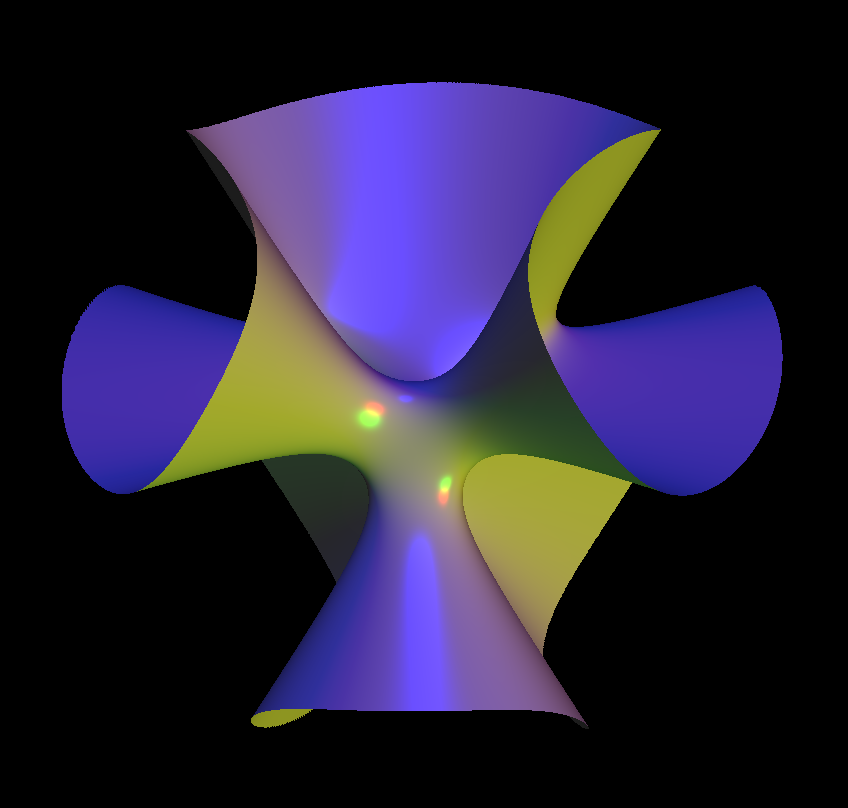

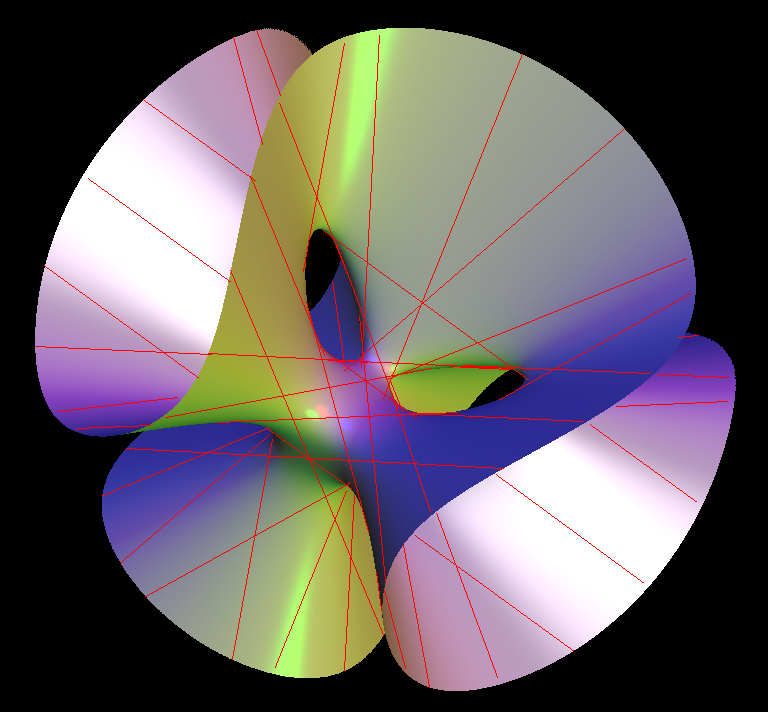
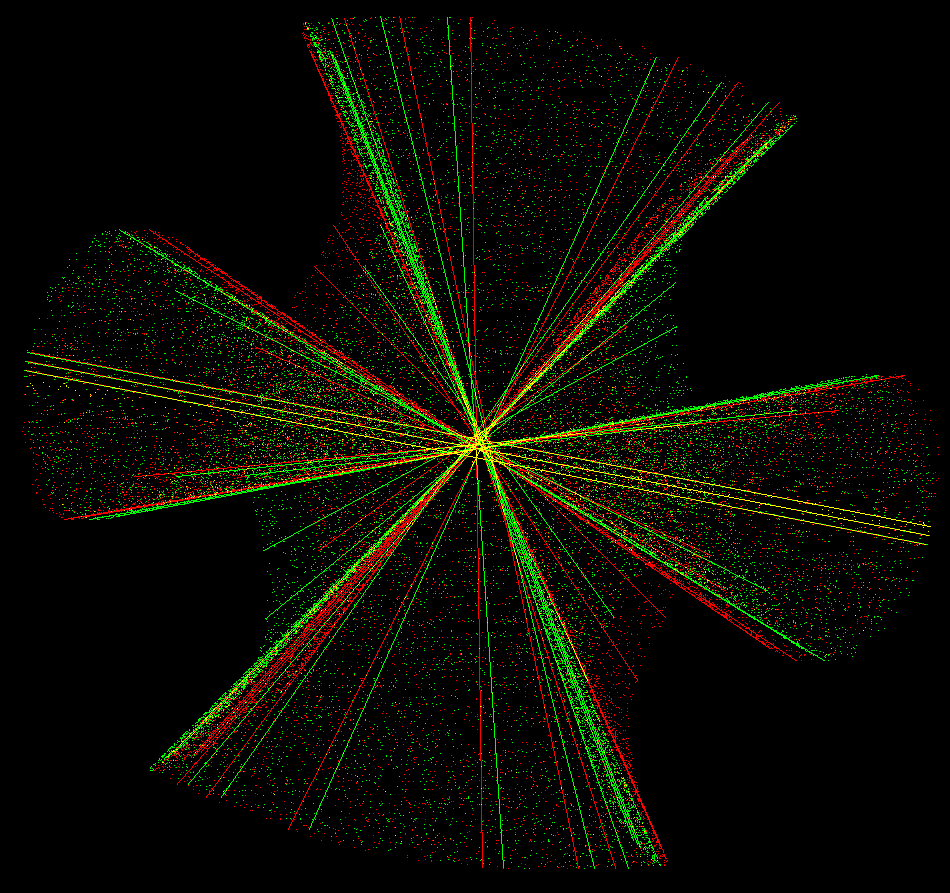
A classical result from algebraic geometry says that on every smooth cubic surface there are 27 exceptional lines (possibly complex). Clebsch Cubic is a surface that has all 27 real lines.
Its function is:
81*(x^3 + y^3 + z^3) - 189*(x^2*y + x^2*z + y^2*x + y^2*z + z^2*x + z^2*y) + 54*(x*y*z) + 126*(x*y + x*z + y*z) - 9*(x^2 + y^2 + z^2) - 9*(x + y + z) + 1
the Clebsch diagonal cubic surface, (aka Klein's icosahedral cubic surface ) the Clebsch diagonal cubic surface do not have singular points.
The Clebsch surface is defined as the set of points (x0:x1:x2:x3:x4) of 4 dimensional projective space P^4 satisfying the equations
x0 + x1 + x2 + x3 + x4 == 0x0^3 + x1^3 + x2^3 + x3^3 + x4^3 == 0Eliminating x0 shows that it is also isomorphic to the surface
x1 ^ 3 + x2 ^ 3 + x3 ^ 3 + x4 ^ 3 = ( x1 + x2 + x3 + x4 ) ^ 3
in P ^ 3.
The symmetry group of the surface is the symmetric group S5 of order 120, acting by permutations of the coordinates (in P4). Up to isomorphism, the Clebsch surface is the only cubic surface with this automorphism group. Properties
The 27 exceptional lines are:
The 15 images (under S5) of the line of points of the form (a : −a : b : −b : 0). The 12 images of the line though the point (1:ζ: ζ2: ζ3: ζ4) and its complex conjugate, where ζ is a primitive 5th root of 1.
The surface has 10 Eckardt points where 3 lines meet, given by the point (1 : −1 : 0 : 0 : 0) and its conjugates under permutations. Hirzebruch (1976) showed that the surface obtained by blowing up the Clebsch surface in its 10 Eckardt points is the Hilbert modular surface of the level 2 principal congruence subgroup of the Hilbert modular group of the field Q(√5). The quotient of the Hilbert modular group by its level 2 congruence subgroup is isomorphic to the alternating group of order 60 on 5 points.
Like all nonsingular cubic surfaces, the Clebsch cubic can be obtained by blowing up the projective plane in 6 points. Klein (1873) described these points as follows.
If the projective plane is identified with the set of lines through the origin in a 3-dimensional vector space containing an icosahedron centered at the origin, then the 6 points correspond to the 6 lines through the icosahedron's 12 vertices. The Eckardt points correspond to the 10 lines through the centers of the 20 faces.


Parts of the content is from Wikipedia Clebsch surface