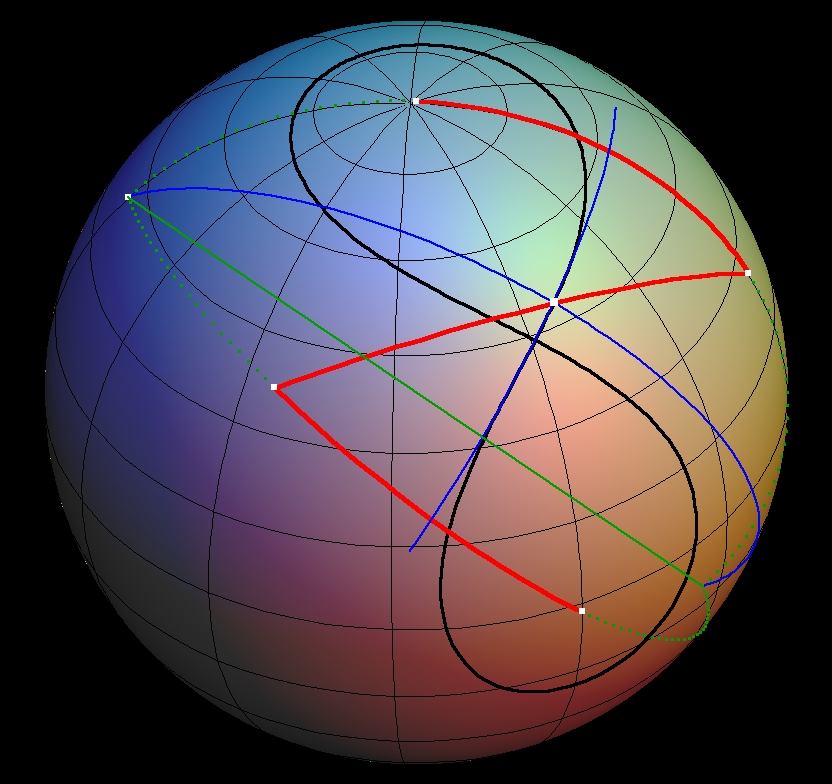

The spherical lemniscate (black) can be drawn by a 3-rod-mechanism in complete analogy to the planar lemniscate.
Of course, on the sphere the rods are great circle arcs (red). The two outside ones can rotate around their free endpoints, the so called foci of the lemniscate. The middle rod is connected to the exterior ones by joints, its midpoint was chosen as the drawing pen.
The tangent construction depends, as in the plane, on the momentary center of rotation of the drawing sphere. The momentary axis of rotation is the green line. Its endpoints on the sphere are found as the intersection points of the green dotted extensions of the exterior drawing rods. Finally, the connection of the drawing pen to the centers of rotation (blue) is the momentary radius of rotation and the tangent (blue) is orthogonal to the radius - the same as for circles.
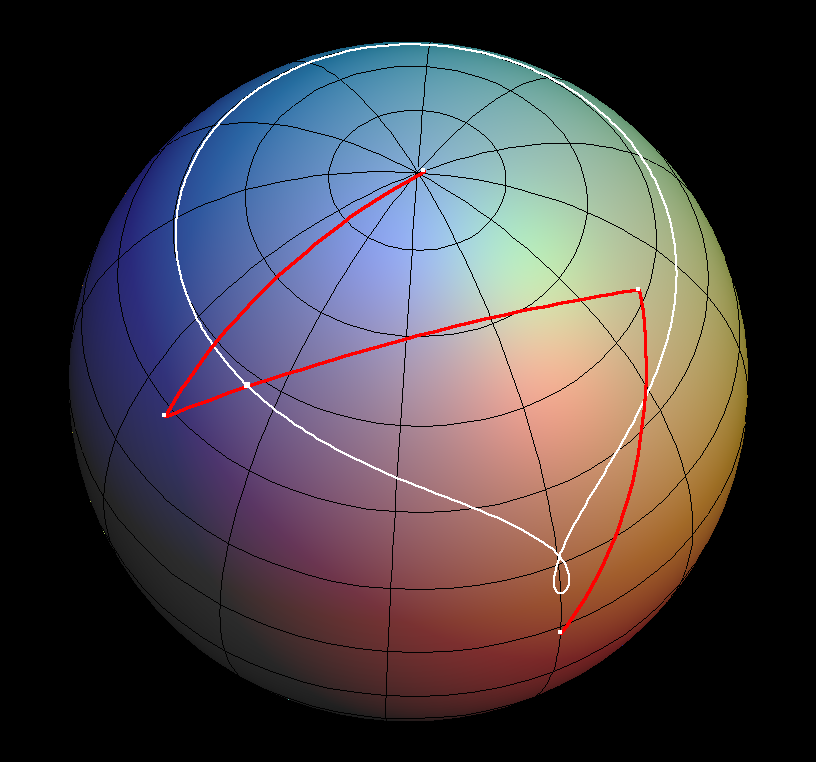
The drawing pen moves on the middle rod and non-symmetric spherical lemniscates are drawn - again similar to the planar case.
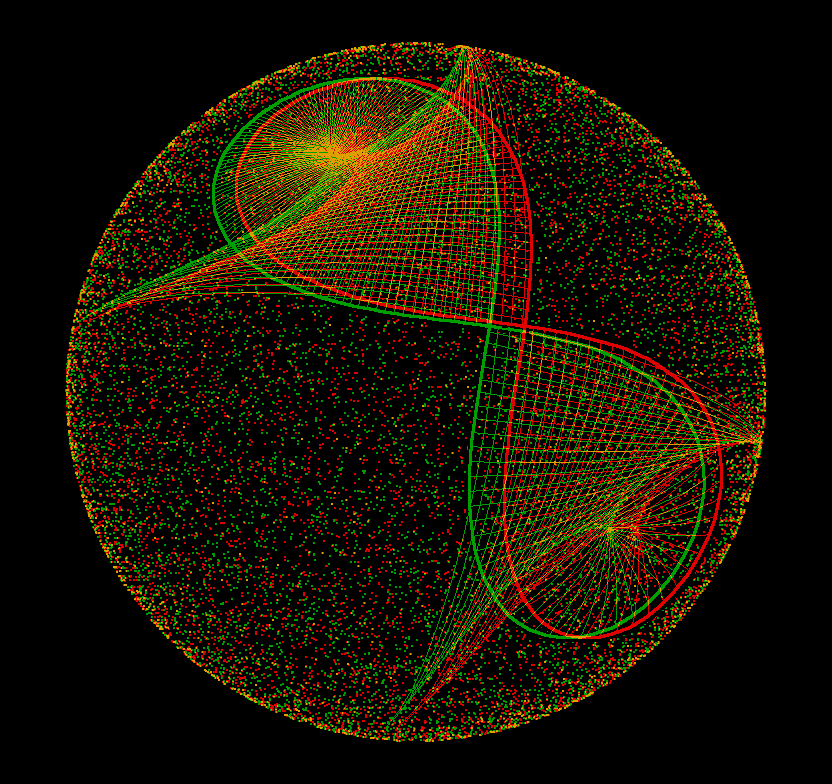

Spherical lemniscate with three osculating circles and the “evolute”, the curve traced out by the midpoints of the osculating circles. The image is a cross-eyed stereo view so that one can see the lemniscate and its osculating circles lying on the dotted sphere. The crossing point of the evolute is the midpoint of the sphere (because the geodesic curvature of the lemniscate is zero at its crossing point).
