Mathematician
Mandelbrot defined this set in order to study the iteration behavior of the family of
quadratic complex functions z ⟶ f(z) := z*z - c. Here c is a complex constant, the so called
family parameter. We explain the initial part of this program in the exhibit
Julia Set.
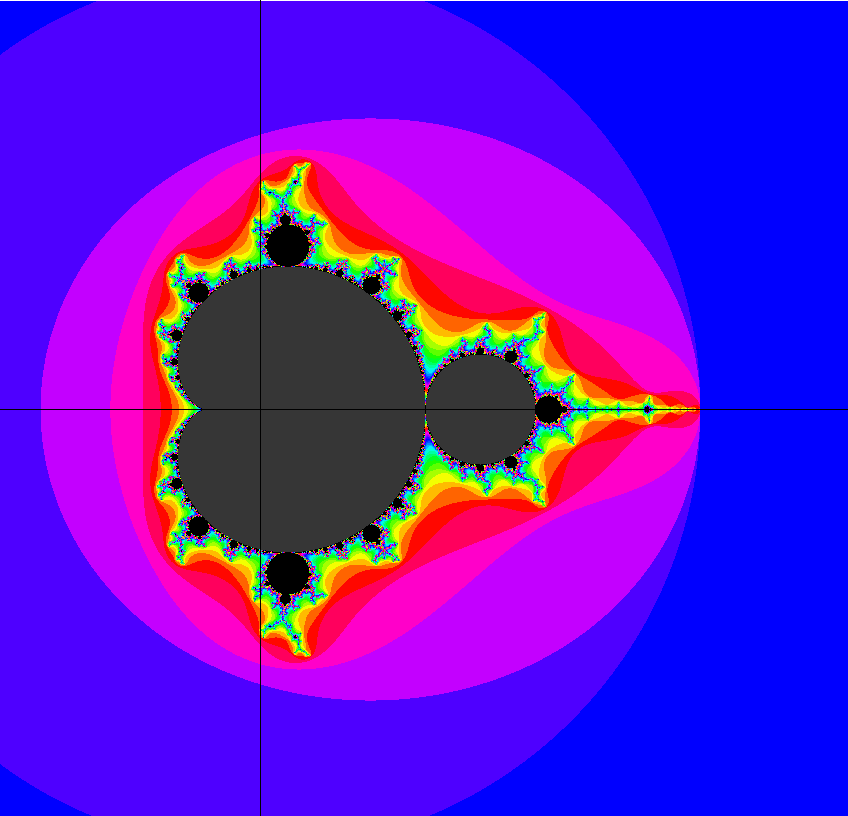
But the Mandelbrot Set M became even more popular outside of mathematics than inside because
it turned out to yield an unlimited collection of wonderful images. These images can be computed
with an extraordinarily simple algorithm due to a theorem of Julia and Fatou from the early
20th century: The points of the Mandelbrot set are exactly those points c in the complex plane
for which the iteration c ⟶ f(c) = c*c - c ⟶ f(f(c)) = square(c*c - c) - c ⟶ f(f…f(c)…))
stays bounded, no matter how often f is applied.
In practise we have only to check whether this sequence gets an absolute value > 2, because
from then on the absolute value increases at every step:
|z| ≥ |c| > 2 implies
|z*z - c| ≥ |z|*|z| - |c| ≥ |z|*|z| - |z| = |z|*(|z| - 1) > |z|
.
Note that
c = 2
implies
f(c) = 4 - 2
so that 2 is in M. For
c = 1
we get f(c) = 0, f(f(1)) = -1,
f(f(f(1))) = 0 = f(1), so that 1 is in M.

The usual fun journeys are to zoom in on various points near the boundary of the Mandelbrot Set and discover an overwhelming richness of formes. This is more fun with a specialized program then with a precomputed sequence in a museum. The more one zooms in the finer structures of M one meets. Therefore one has to look at more terms of the iteration sequence, for example 5000 in our last image. Good specialized programs therefore use more efficient algorithms than the simple one described above. But it is probably that simple algorithm which made the Mandelbrot Set so popular.
