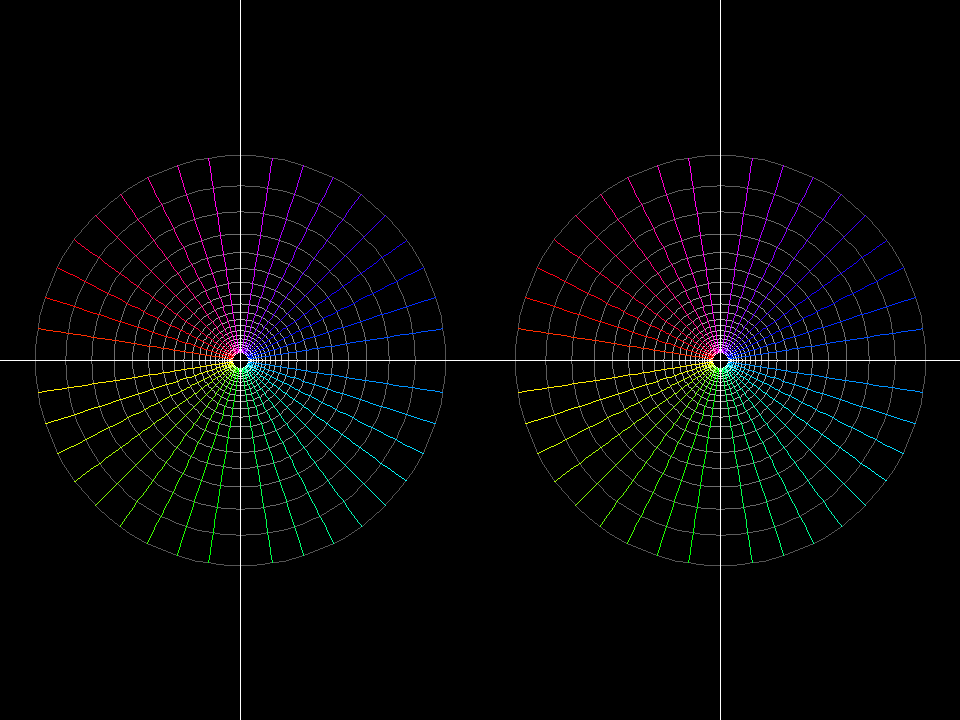
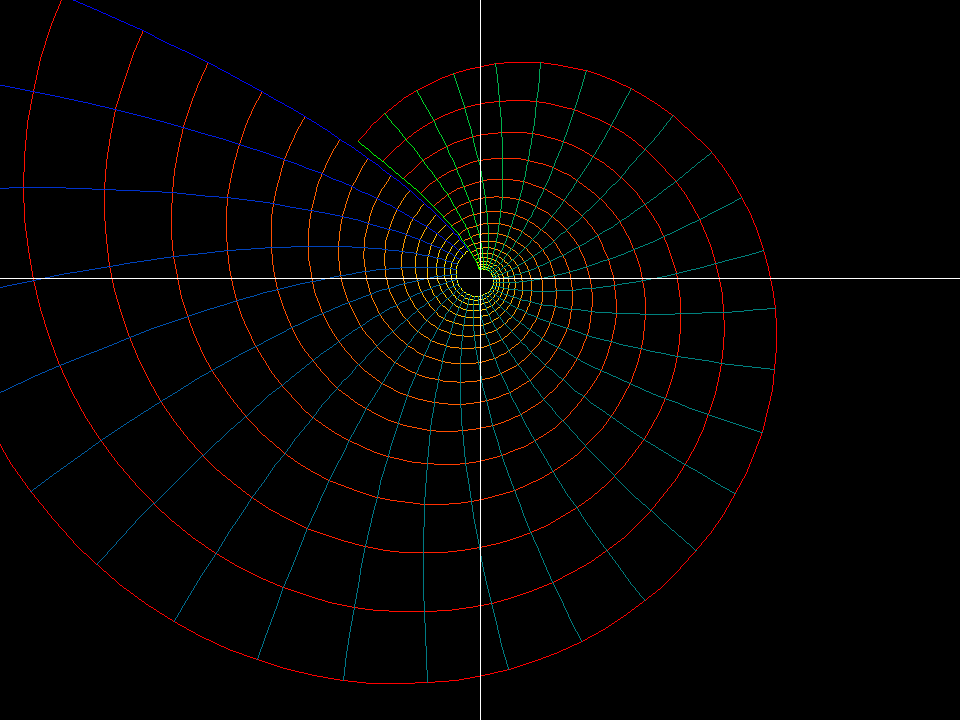
- function:
f(z) = (1+a)*z/(a*z + 1) - domain: polar grid
1/5 < |z| < 5 - morph:
0 < a < 1
A Mobius Transformation (aka fractional linear functions) is this function:
f(z) := (a z+b)/(c z+d)
They differ from the inverse function 1/z
[see Complex Inversion]
by adding translation, rotation and scaling.
Because (for c ≠ 0)
(az+b)/(cz+d) =
a/c * (cz + bc/a)/(cz + d) =
a/c*(cz + d )/(cz + d) + (b - ad/c)/(cz + d)
so that
(az+b)/(cz+d) = a/c + (bc - ad)/c^2 * 1/(z + d/c).
This implies that arbitrary Moebius transformations are not more complicated than f(z) = 1/z. In particular: all Moebius transformations map lines and circles to lines and circles, or just circles to circles when stereographically projected to the sphere.

f(z) = (1+a)*z/(a*z + 1)1/5 < |z| < 50 < a < 1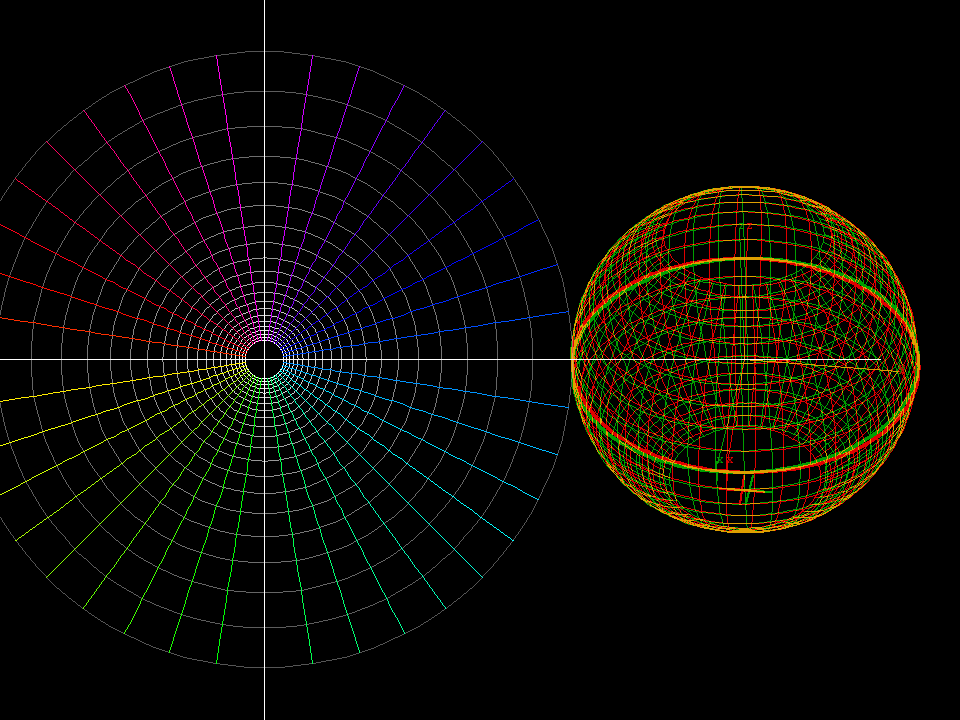
z ⟶ f(z) = (1+a)*z/(z + a)1/4 < |z| < 40 < a < 1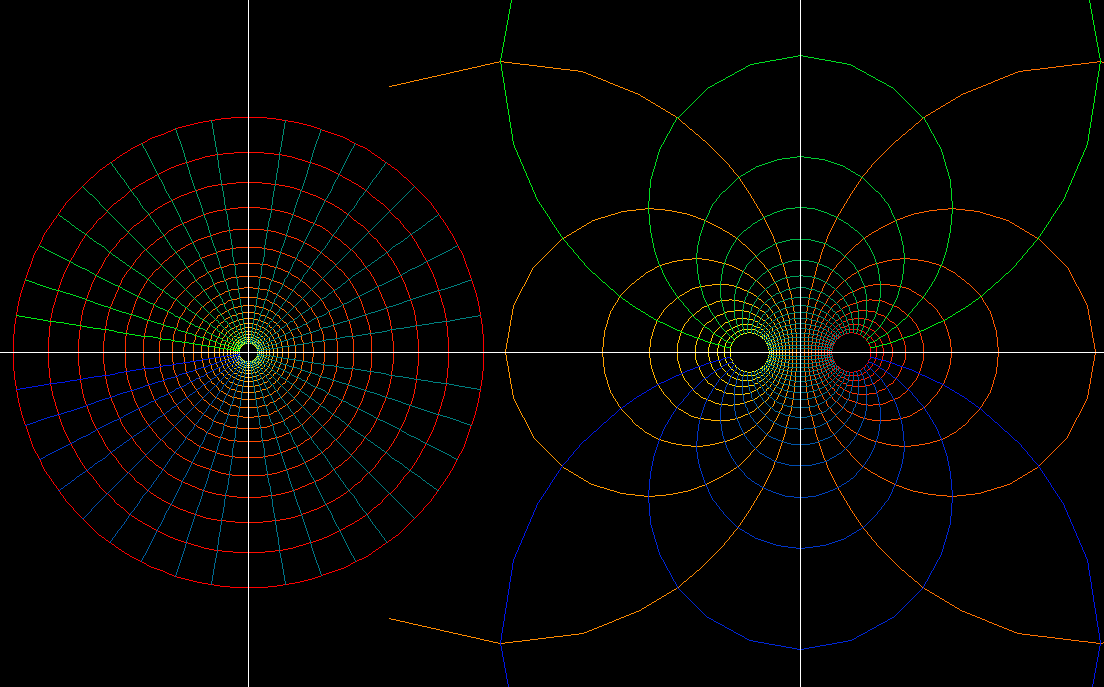
f(z) = (exp(i*c) *z - 1)/(exp(i*c) *z + 1)1/5 < |z| < 50 < c < 2*piAll these moebius transformations map 0 to -1 and infinity to +1. We can view the changing grid lines as “moebius rotation” around -1 and +1. The name is justified because these maps are true rotations when viewed on the Riemann sphere. The inverse function f(z) = 1/z is, on the Riemann sphere, 180 degree rotation around -1, +1. The changing grid lines therefore represent a homotopy from the identity to the inverse function and back to the identity.
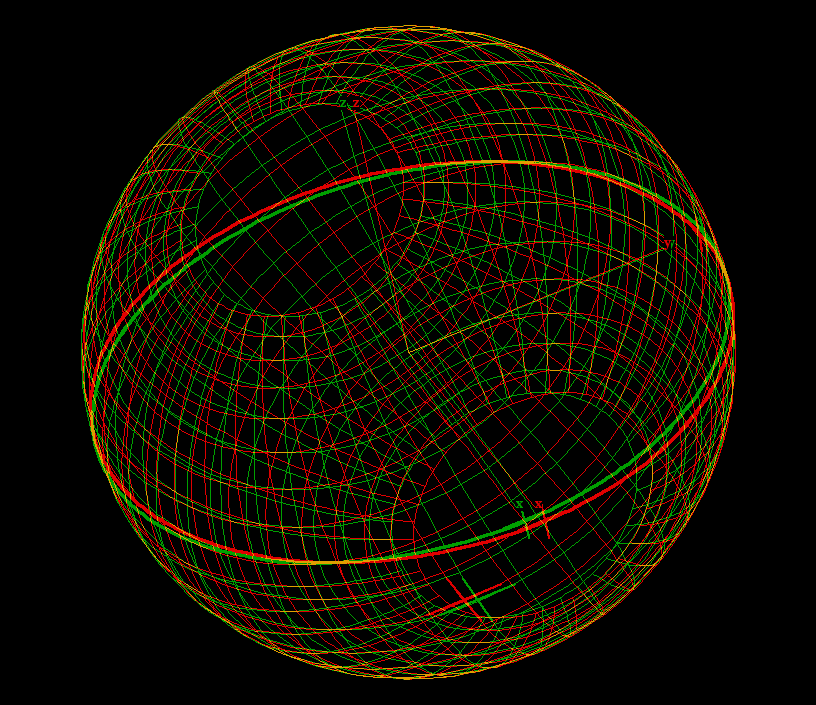
The previous moebius transformations, viewed on the Riemann sphere, are rotations around the x-axis.
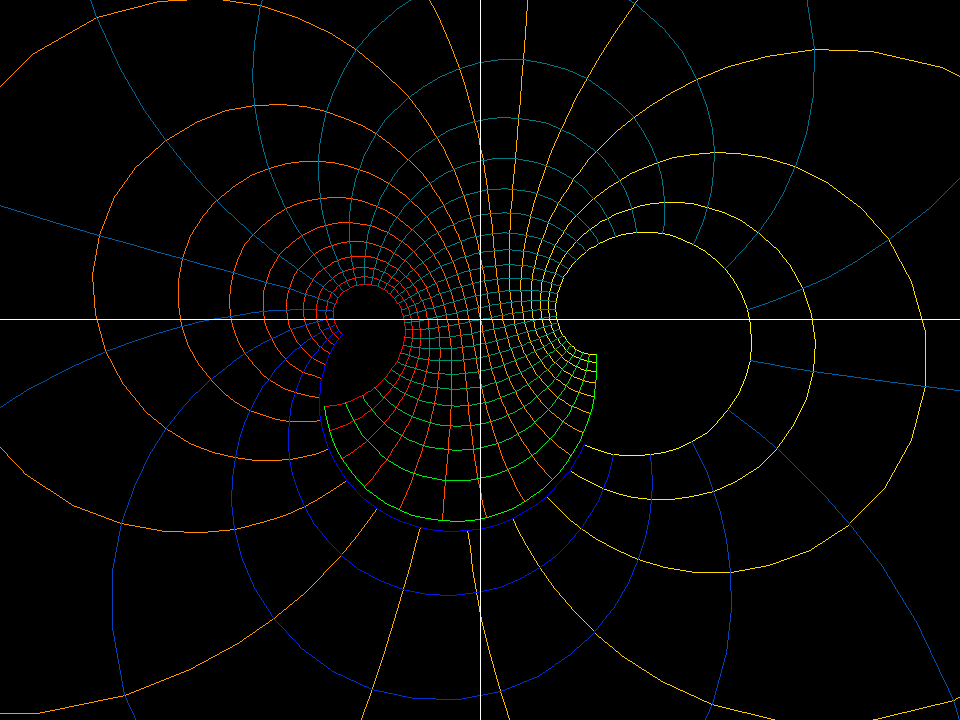
z ⟶ (1 - z)/ (1 + z) to the previous images.