
The function f(z) = log(z) is an inverse of the exponential function: log(exp(z)) = z.
But log(z) cannot be defined as a differentiable function in the full plane for two
reasons:
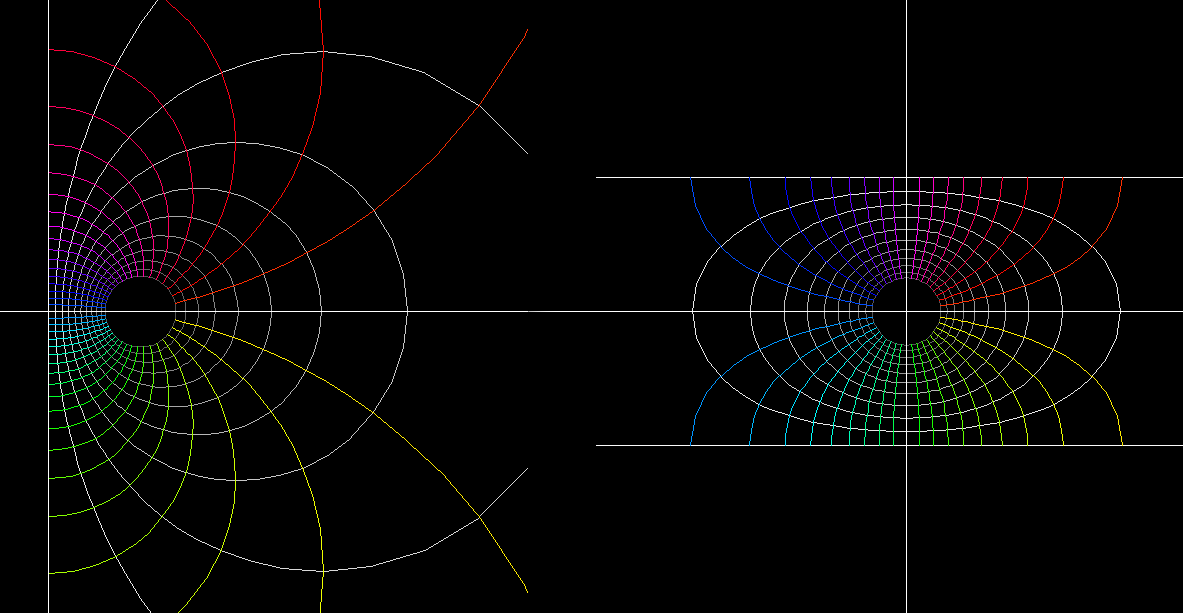
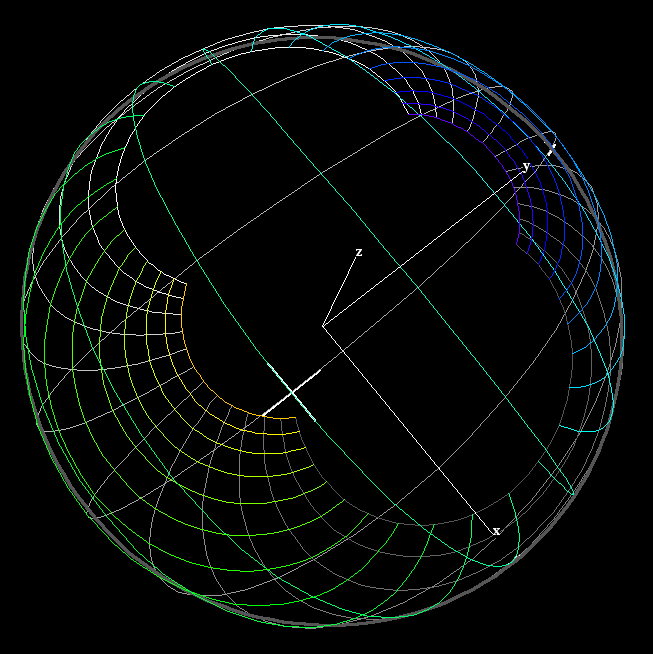
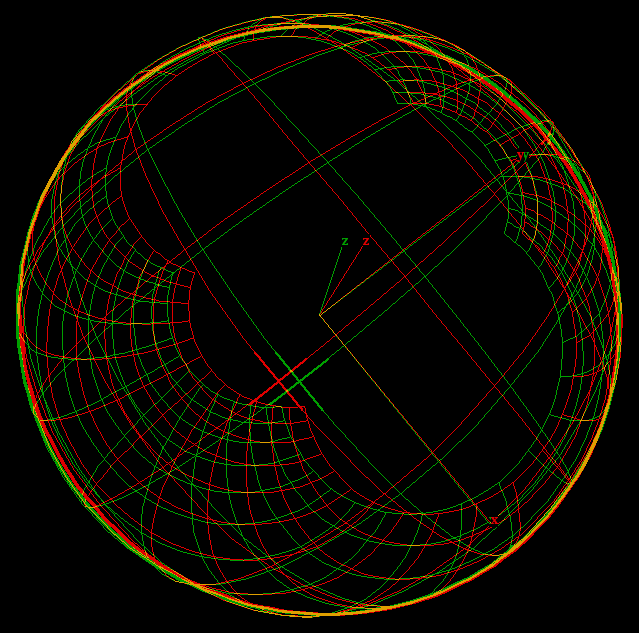
exp(z) is periodic, namely exp(z) = exp(z + 2i*pi). This says that there are infinitely many choices for defining the logarithm of w = exp(z), namely log(w) = z, = z + 2i*pi, = z + 4i*pi …. , log(w) = z + n*2i*pi, n integer.The “principal value” of the complex logarithm is a differentiable function defined on the plane minus the negative real axis. The values of this function lie in the horizontal strip { z ; -pi < Im(z) < +pi }.
Nothing special happens on the negative real axis. One can define the complex logarithm as a differentiable function on the plane minus any half line from zero to infinity. The animation shows some choices.
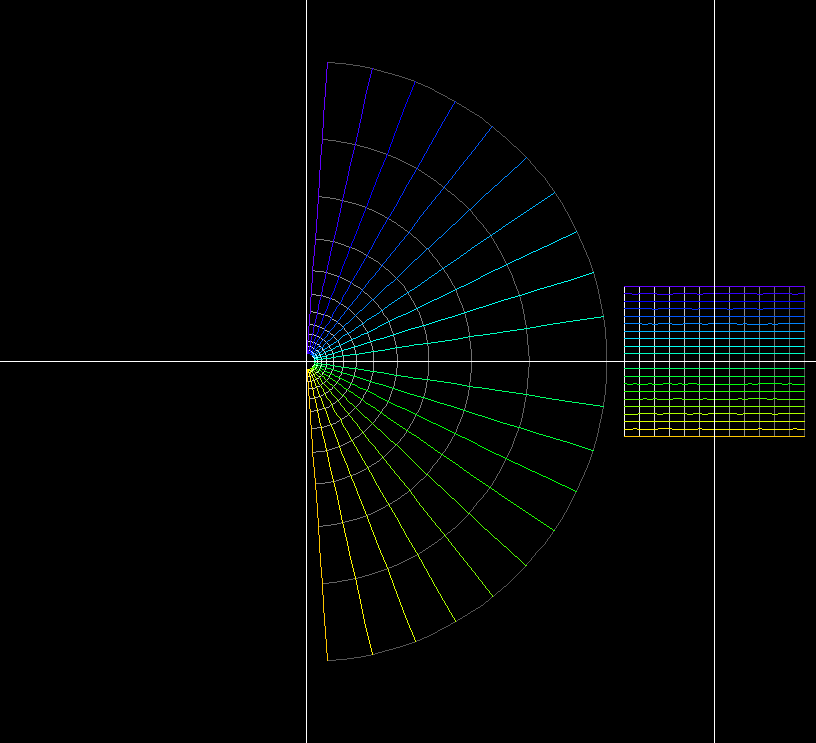
log(z)
log(z) is the inverse function of exp(z).
[see Complex Exponential Function]
exp is a periodic function, log cannot be defined as a differentiable function on the whole plane. The “principal value of log” is a differentiable function in the plane minus the negative real axis. The other values of log differ from the principal value by an integer multiple of 2 π. Since every z ≠ 0 has multiple logarithm values, the complex logarithm is called a “multivalued” function.