The exponential function is defined by its differential equation exp'(z) = exp(z) with the initial value exp(0) = 1.
For no real number x ≠ 0 can exp(x) be computed in finitely many steps. All the numbers which our computers give us are only approximations of the true value of exp(x).

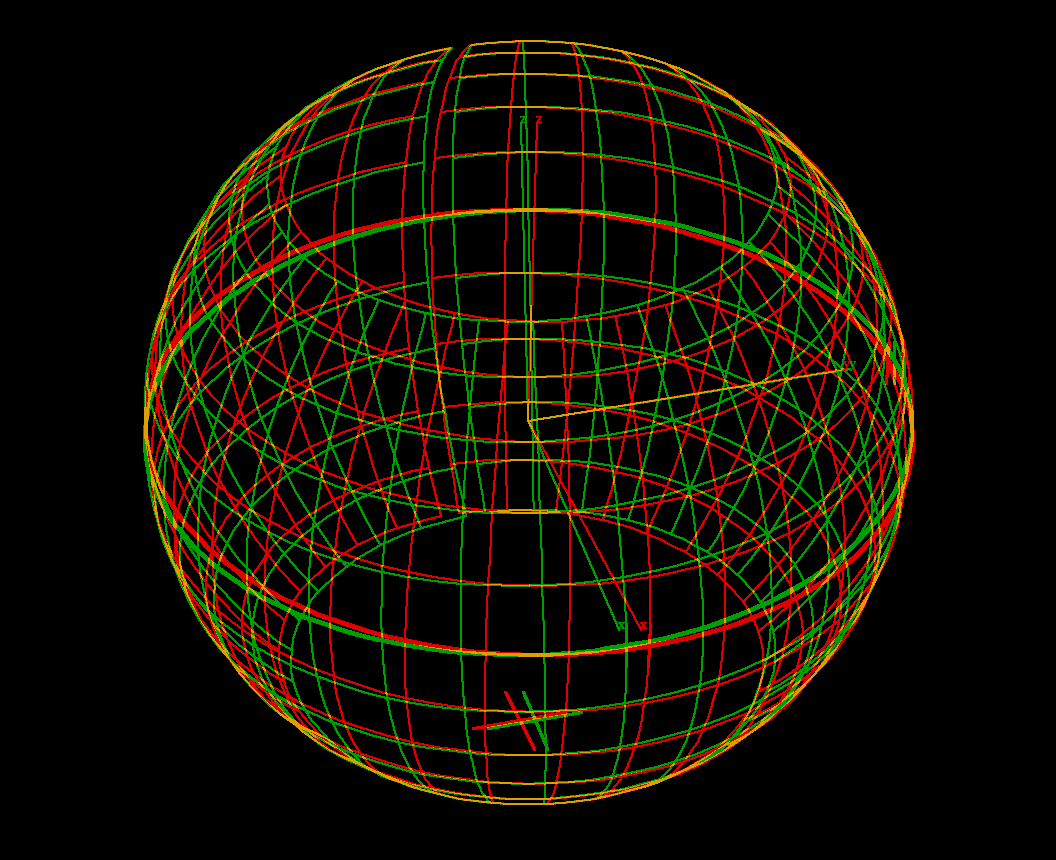
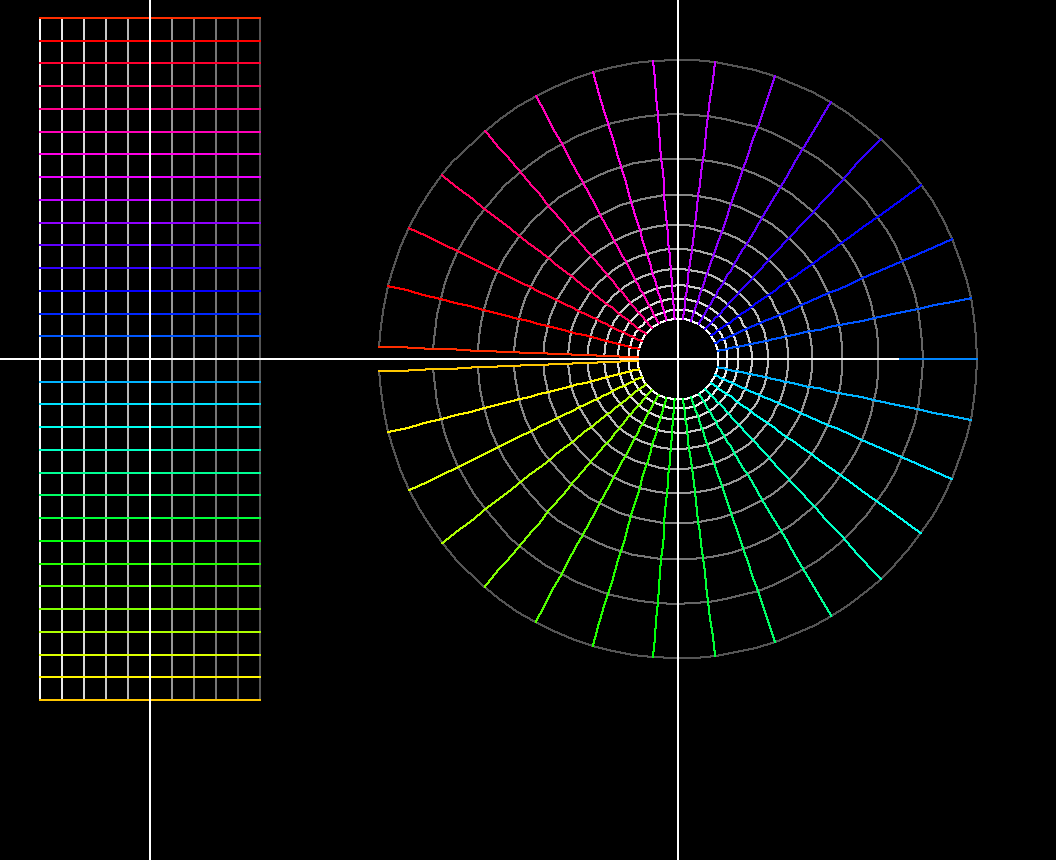
z → exp(a*z) = e^(a*z)1 → 1+0.4*i-1 ≦ Re(z) ≦ 1; -3.1 ≦ Im(z) ≦ 3.1If Im(a) > 0 then the gridlines are spirals. The exponential function is periodic: exp(z + 2 π * i) = exp(z). One can see that in the range: For a = 1 the circular grid lines are about to close. The periodicity is also clear from the formula:
exp(x + i * y) = exp(x) * (cos(y) + i * sin(y))
.
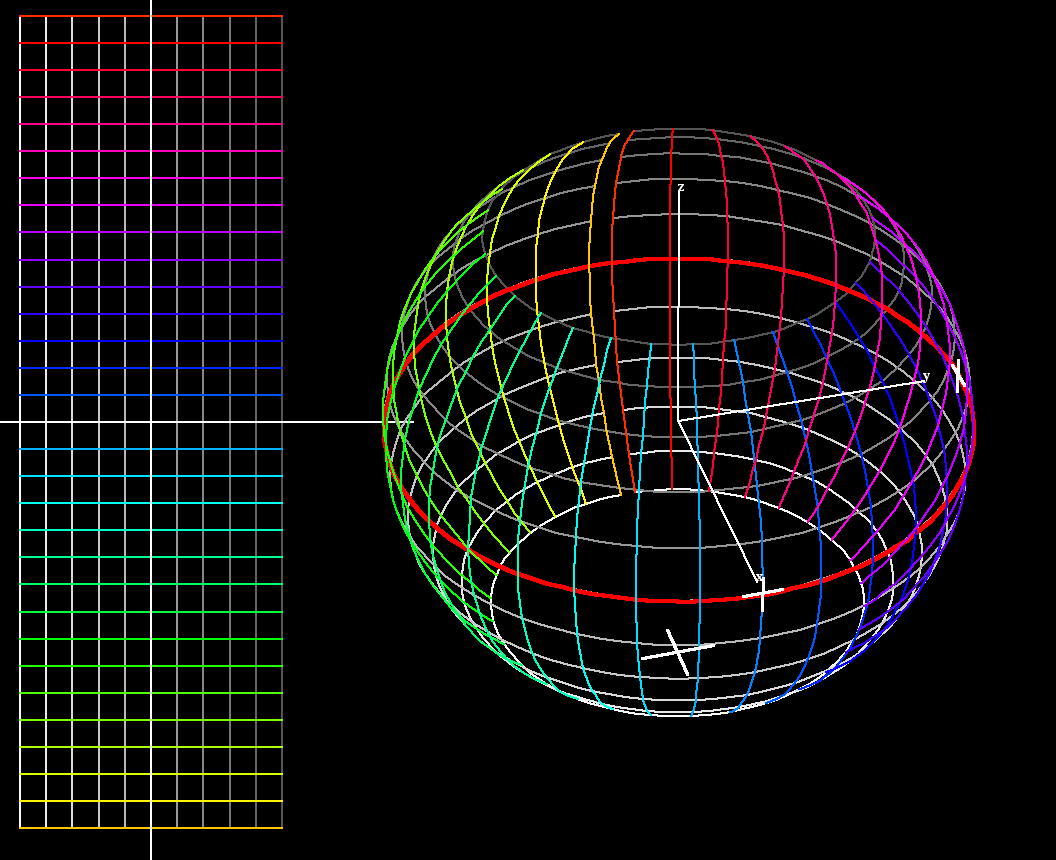
e^(a * z)a : 1 to 1+0.4 * i-1 ≤ Re(z) ≤ 1; -3.1 ≤ Im(z) ≤ 3.1Each gridline intersects all the meridians with the same angle, such curves are called loxodromes.