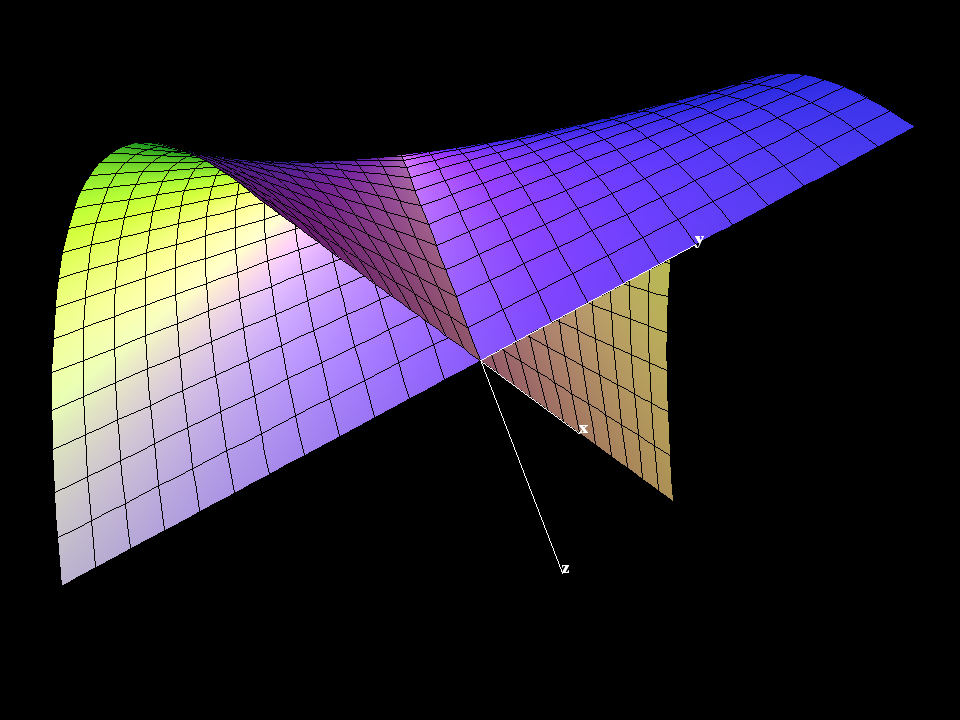

The name umbrella comes from the fact that the implicit equation
x^2 - y^2 * z = 0 has the surface plus the z-axis
(like a handle) as solution.
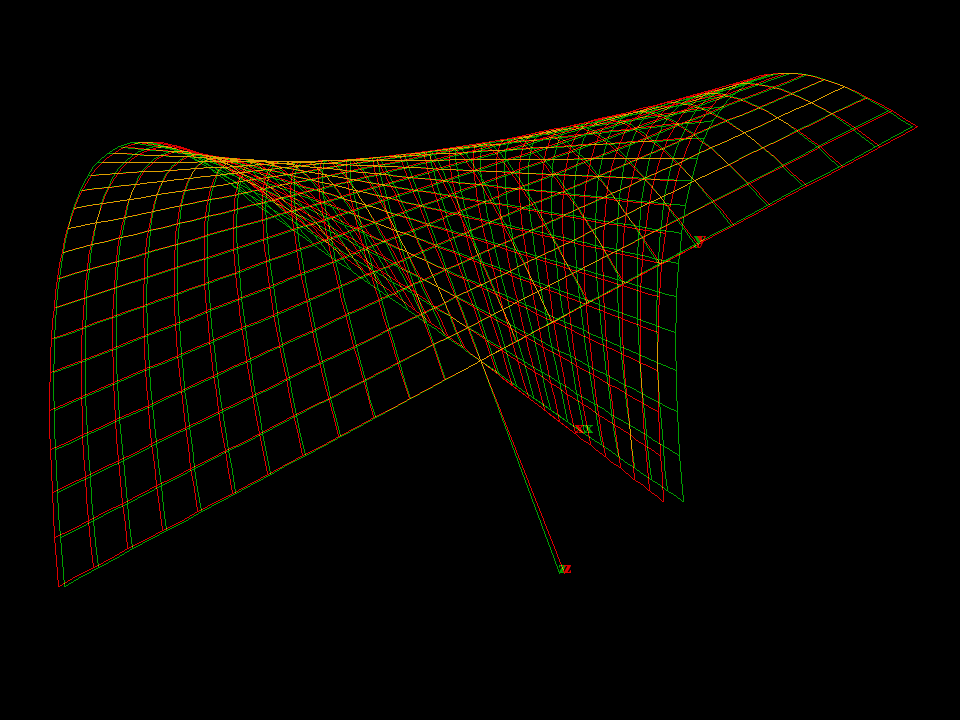
Strictly speaking, the Whitney umbrella is the algebraic surface defined by the implicit equation:
x^2 - y^2*z == 0
It has two algebraic components, a two-dimensional piece that is given parametrically by the equations:
x := u * v y := u z := v * v
and a one-dimensional piece, namely the entire z-axis (the handle of the umbrella). The two-dimensional part is important in the theory of singularities. The point at the end of the line of self-intersections is a singularity of a type called a pinch point. This is a canonical representative of the only stable singularity for mappings from R^2 to R^3.