The plane and the sphere are the most symmetric surfaces and they have much in common. Usually we accept planes without definition while a sphere is defined as the set of all points in R^3 that have the same distance r from a so called midpoint. r is called radius of the sphere. If we choose the origin as midpoint then the Pythagorean theorem says that the sphere can be described by the equation:
x^2 + y^2 + z^2 = r^2
Great circle arcs (at most half way around) are the shortest connections between points on the sphere - they therefore play the same role for the sphere that straight lines play for the plane. In particular we have the same kind of triangle geometry on the sphere that we know from the plane. For example in the plane, a formula, called cosine law, computes the angles from the edge lengths:
c^2 = a^2 + b^2 - 2 a b cos(γ)
A more complicated looking formula does exactly the same for triangles on the unit sphere:
cos(c) = cos(a)*cos(b) + sin(a)*sin(b)*cos(γ)
For very small a,b,c the Taylor approximations of the trigonometric functions:
cos(x) = 1- x^2/2 + O(x^4), sin(x) = x + O(x^3)
get us back to the Euclidean formula:
1 - c^2/2 = (1 - a^2/2)*(1-b^2/2) + a b cos(γ) + fourth order errors
A striking difference between plane and sphere is the absence of scaling similarities on the sphere. In fact, the area of a great circle triangle with angles (α, β, γ) can be computed from the angles alone:
area = α + β + γ - π.
This can be seen from the above picture if one knows already the area of a diangle, i.e. of the part of the sphere between two great circles meeting with the angle α. We have area = 2*α. The great circle triangle determines three such diangles with respective angles α, β and γ. These three diangles and their antipodes cover the triangle and its congruent antipodal triangle three times and the rest of the sphere just once. This says:
(area of sphere) + 4*(area of triangle) = twice the sum of area of the 3 diangles
or
4*π + 4*(area of triangle = 4*(α + β + γ)
as claimed.

The sphere is almost always parametrized with so called “geographical” or “spherical”
polar coordinates. Geographers measure the latitude from the equator, i.e. between
-π/2
and
π/2
.
Mathematicians treat the latitude as a spherical radius and therefore start
with zero from the pole. Abreviate u = latitude from 0 to π, v = longitude from 0 to 2π.
Then
x = sin(u)*cos(v),
y = sin(u)*sin(v),
z = cos(u)
The most important maps from or to the sphere are:
And, again from Archimedes, volume comparison of cylinder, cone and half sphere.

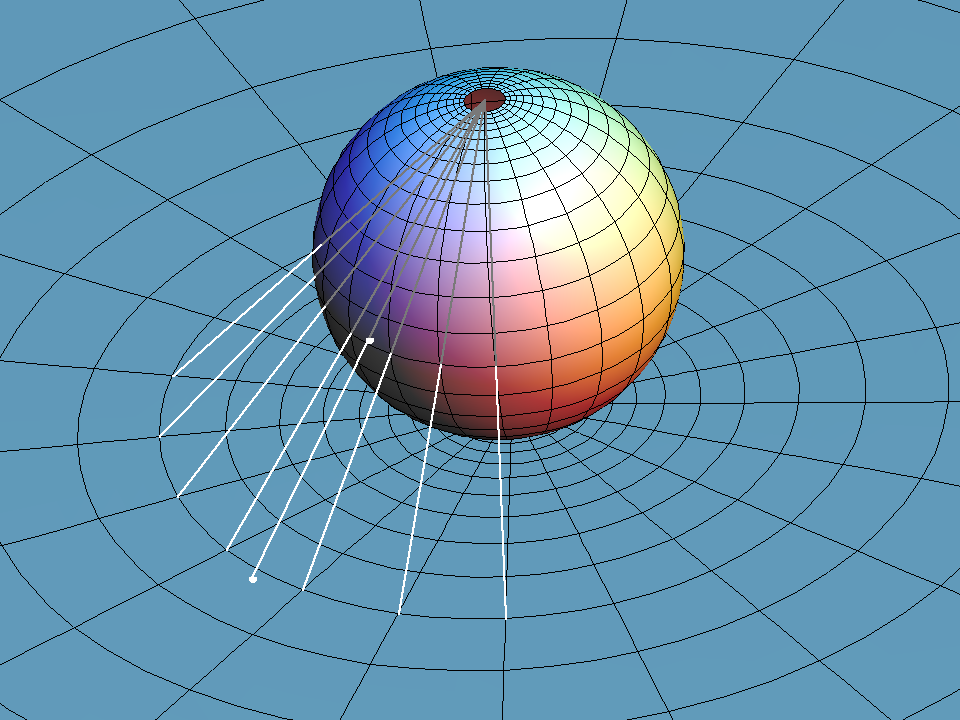
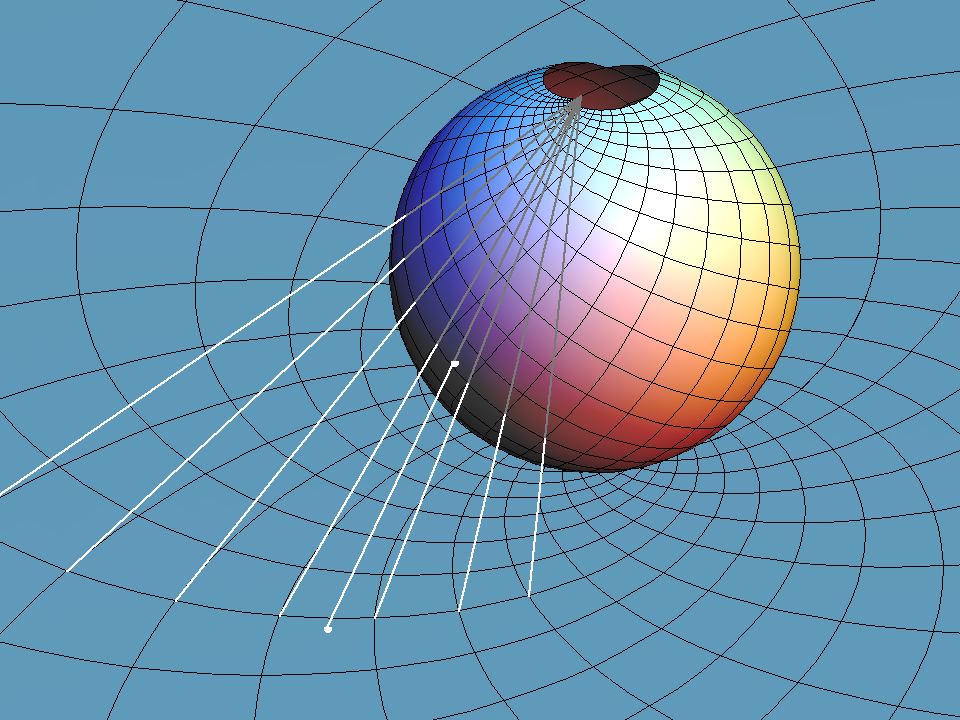
Stereographic projection is the projection of the sphere from one point to the tangent plane at the antipodal point. We call the projection center “south pole”. The stereographic image of a circle through the south pole is a straight line (see image), namely the intersection of the circle plane with the image plane. Observe that the image line is parallel to the tangent of the projected circle at the south pole. This says: Two circles through the south pole intersect with the same angle as the image lines of the two circles.
This almost proves: stereographic projection is angle preserving.
We only need to add: every tangent to the sphere (not at the south pole) is tangent to a unique circle through the south pole. Why is that true? Take the (unique) plane which is spanned by the south pole and by the given tangent to the sphere. Intersect this plane with the sphere to get the desired circle through the south pole.

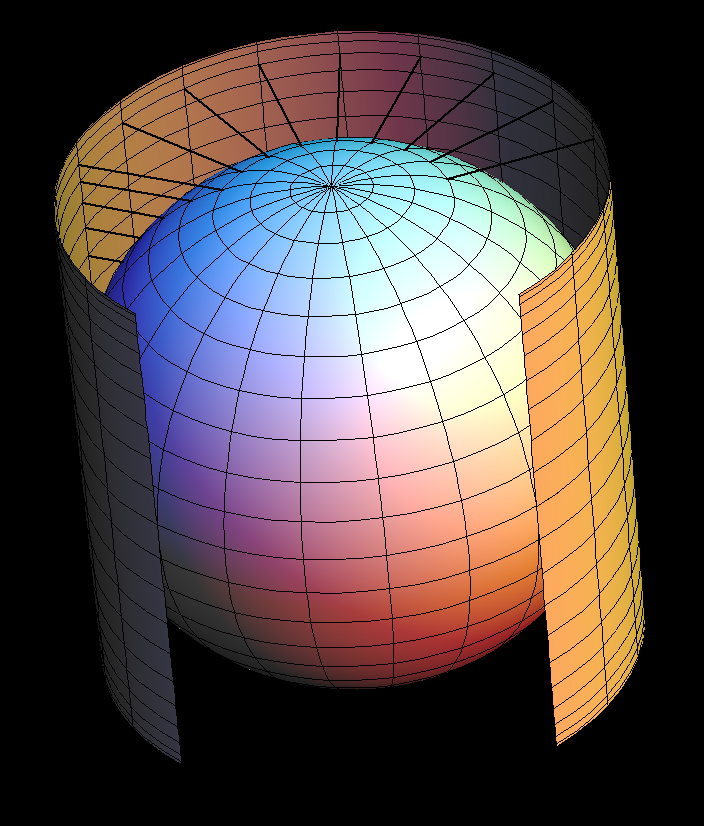
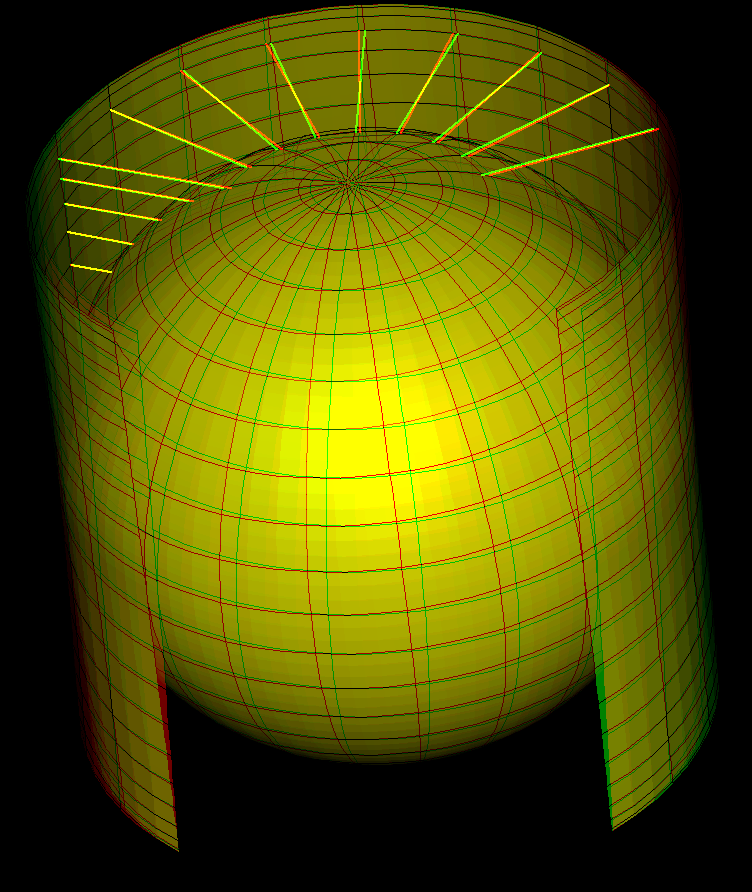
Archimedes has observed that the radial horizontal projection from a cylinder, that touches a sphere along the (horizontal) equator, is area preserving. This implies immediately that the unit sphere has area 4 π.
Proof:
If u is the polar angle from the north pole then a latitude circle is at height cos(u) above the equator and has radius sin(u). It is shorter by the factor sin(u) than the (preimage-) latitude circle on the cylinder (radius = 1).
The vertical lines on the cylinder are mapped to the longer meridians on the sphere. These vertical lines are not stretched uniformly, but at height cos(u) they are locally stretched by the factor 1/sin(u) - because the vertical line and the sphere tangent to the meridian at height cos(u) intersect with angle u.
This shows: Archimedes projection shortens horizontal directions by the factor sin(u) and stretches vertical directions at height cos(u) by the factor 1/sin(u). And sin(u) * 1/sin(u) = 1 means: the projection is area preserving.