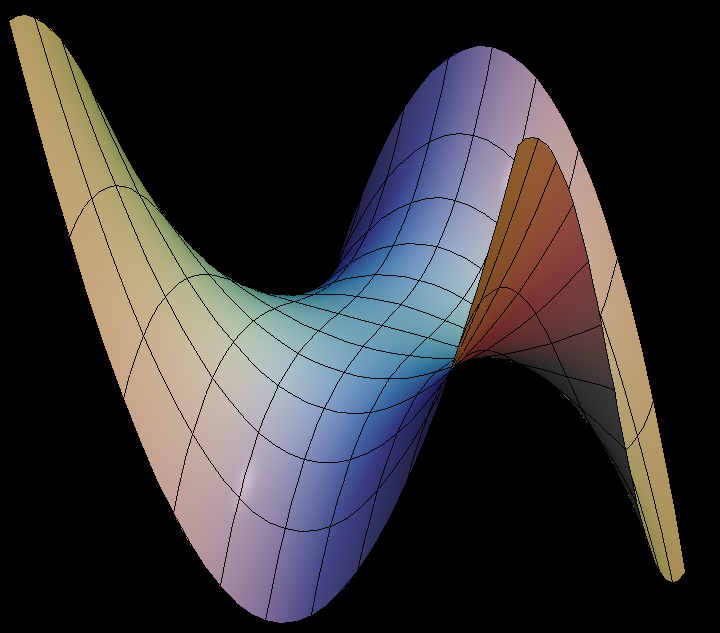

The surface is the graph of the function
(u,v) ⟶ f(u,v) = u^3 - 3uv^2
The first and second derivatives of the function vanish at (0,0). This produces an unusual saddle which goes down in 3 directions and therefore allows a monkey to ride it with the tail down.
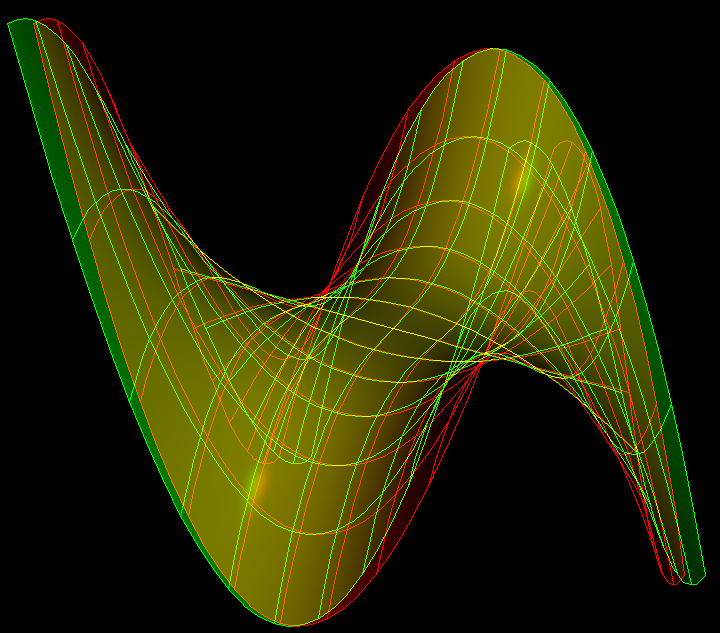
Monkey Saddle is a surface that demonstrates a saddle-shaped surface with three down slopes. It is named as if for a monkey to sit on and for his tail to rest. This surfaces is used to illustrate that a surface can have a saddle-like shape with n alternating upward and downward slopes around a point, where n is greater 2.