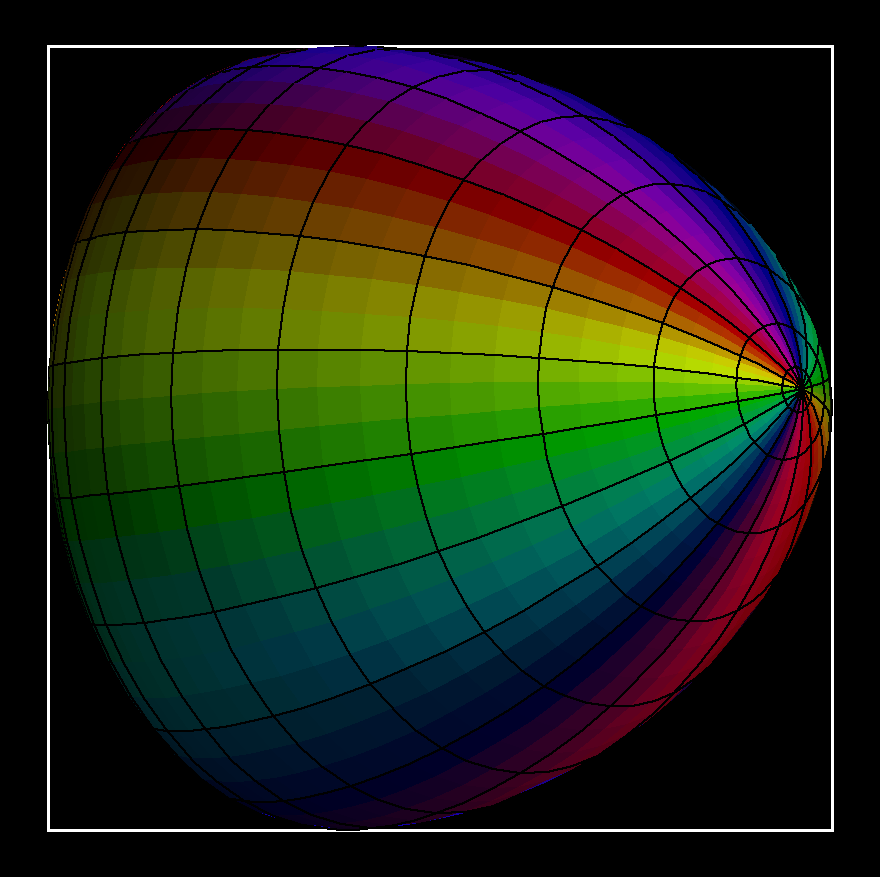
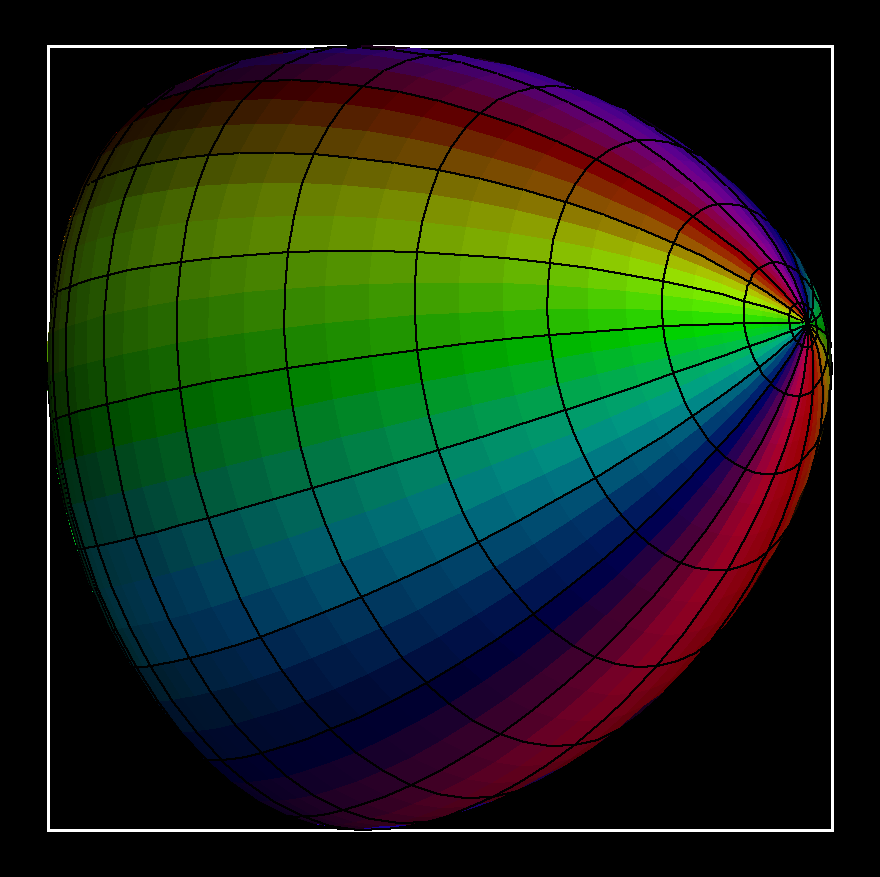
A convex surface which has in every direction the same diameter is called “surface of constant width”. The diameter in any given direction is the distance between the two (opposite) tangent planes orthogonal to that direction.

Surfaces of constant width can move around in a cubical box which they touch at all six faces. This “rotation” is more a wobbling around since no “midpoint” stays fixed.
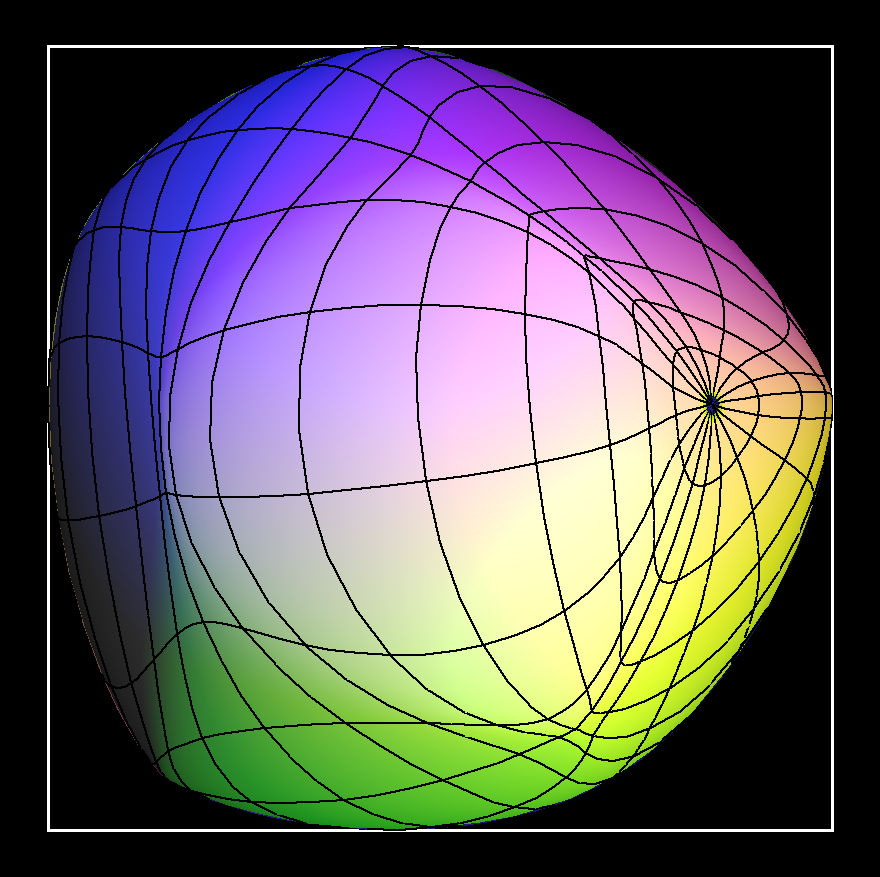
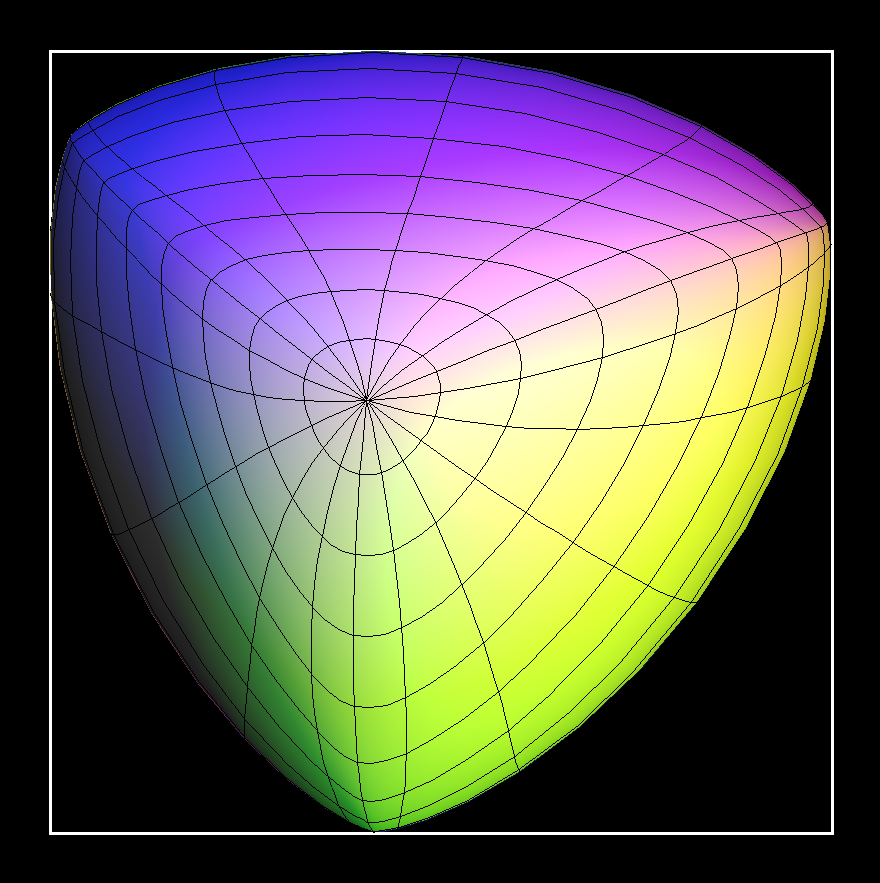
A convex surface, given as the image of a map F: S^2 ⟶ R^3, can be defined by its "support function" h : S^2 ⟶ R+ by putting for each vector n in S^2
F(n) = h(n) * n + grad h(n)
(grad h understood as tangent vector of S^2)
The vector n is the exterior normal of the surface at the point F(n).
The image of F is a surface of constant width w, iff h(n) + h(-n) = w.
If we write
n = (x,y,z) with x^2 + y^2 + z^2 = 1
, then we take
h(x,y,z) = a + b*z^3 + c*xy^2 + d*yz^2 + e*xz^2 + f*xyz + g*xy^2z^2
The first constant a has to be large enough so that the values of h are positive.