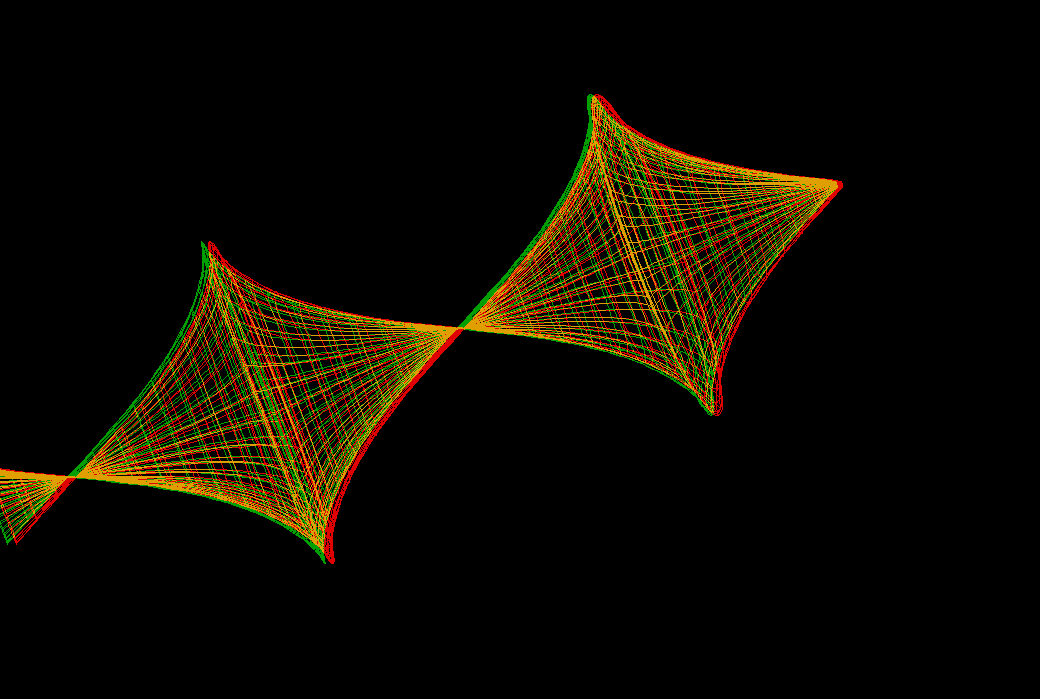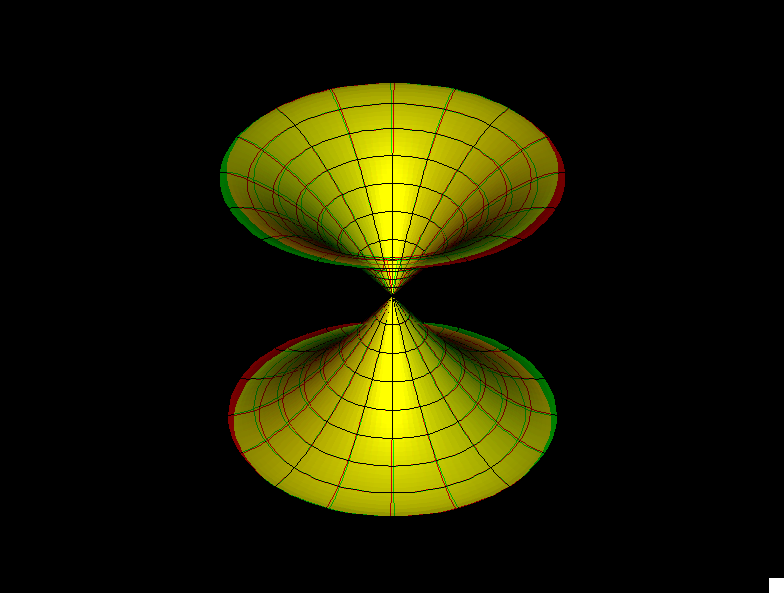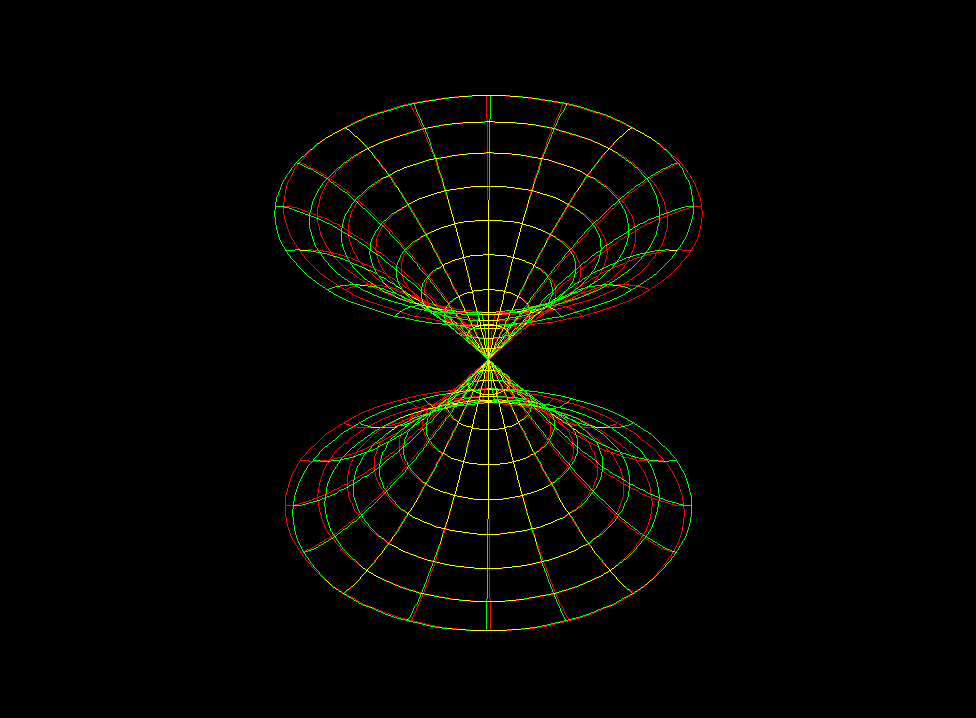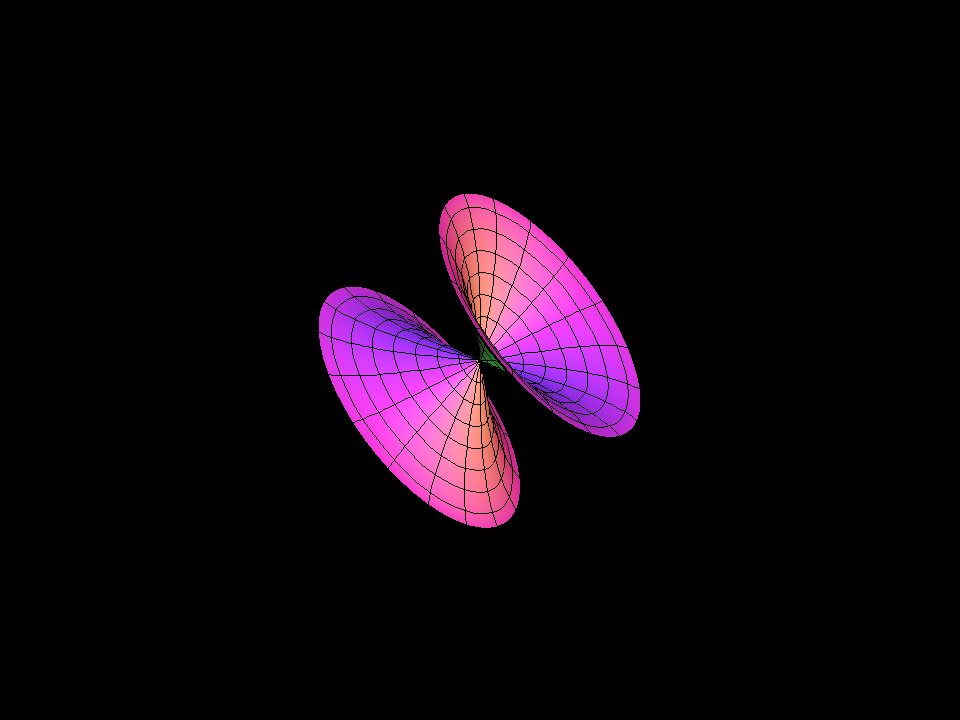

One half of these surfaces (cut in the middle) converge to the Pseudosphere
The formulas for the meridians of the surfaces of revolution with Gauss curvature
K = -1
are explicit and well known. To deform these surfaces, keeping
K = -1, it is more
convenient to construct these surfaces from solutions of the Sine-Gordon equation (SGE).
For surfaces of revolution these SGE solutions can be obtained from the ODE
q''(u) = sin(q(u))
, with skew-symmetric solutions defined by initial conditions
q(0) = 0q'(0) = b > 0Then one can do the same as in the classical Dini deformation: define new solutions
qn(u,v) := q(cosh(d)*u + sinh(d)*v)
, with d the Dini parameter. The animation shows these surfaces.