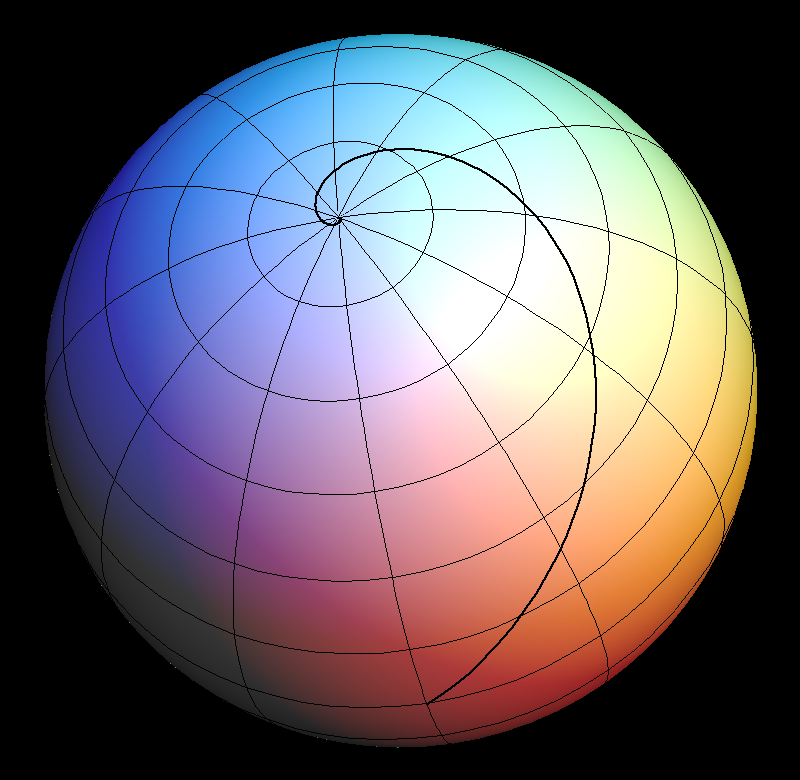

loxodromes are spherical curves which intersect the longitudes (hence also the latitudes) under a constant angle. In a mercator map of the sphere these curves are straight lines. To stear a shortest course across the ocean requires regular position measurements. By contrast, to stear a loxodromic course one only needs to keep the angle against the north direction constant. The animation shows 10 loxodromes from the equator towards the north pole.


A loxodrome (also called a rhumb line) is a route that a boat would take if it kept a constant compass heading (so that on a Mercator projection it is simply a straight line). To be more formal, a loxodrome is a path that lies on the unit sphere in R^3 and that makes a constant angle with the great circles of longitude. Thus the loxodromes are analogous to the logarithmic spirals in the complex plane, which make a constant angle with the rays through the origin. In fact, since sterographic projection from the complex plane to the unit sphere is conformal (and in particular angle-preserving) and since the stereographic projection of the radial lines in the plane are the circles of longitude, it follows that the loxodromes are given by stereographically projecting the logarithmic spirals. On the other hand, since the exponential map of the complex plane to itself is conformal and maps the lines parallel to the real axis to the radial lines, it follows that the logarithmic spirals are just the images under the exponential map of straight lines, i.e., the images of the maps t → aa*t + i t .
Hence we can define the loxodromes parametrically by
t → StereographicProjection(Exponential(aa*t + i t))