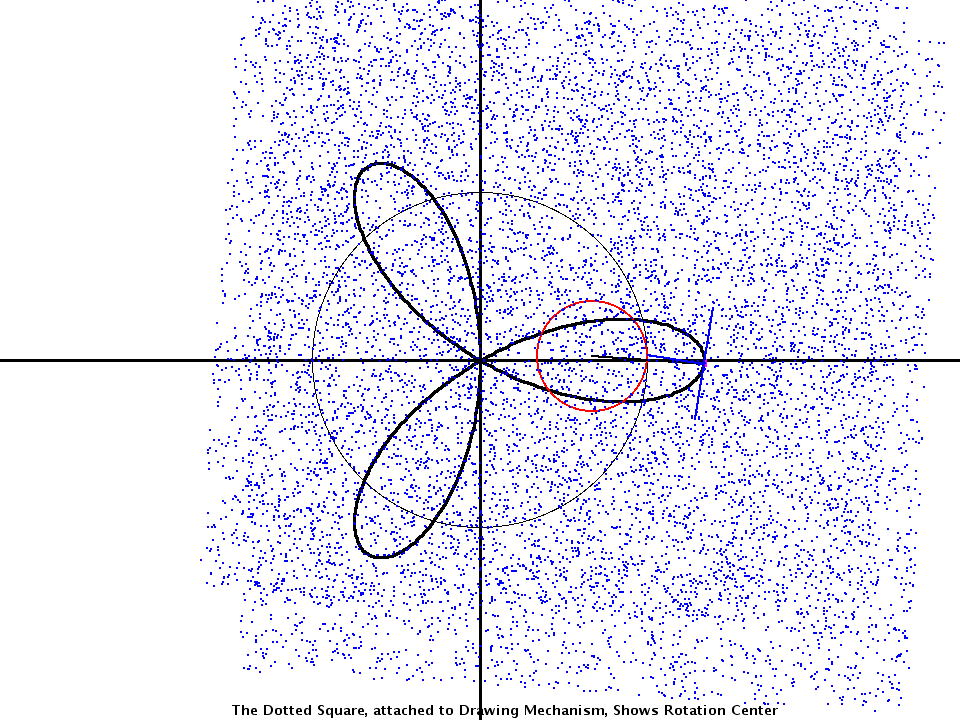
Epicycloids and Hypocycloids
Positive frequencies let the circle role outside

Modify the curve

frequency, -12 ... +12:


stick, 0 ... 5:








The curves are defined by these equations:
c(t) = [ RR * cos(t), RR * sin(t) ] +
[ sticklength*cos(frequency*t),
  sticklength*sin(frequency*t)];
The curve and ists tangents are obtained from a rolling construction.
If sticklength = RR/|frequency| (stick = 1), the curves are called epicycloids - which roll outside - and hypocycloids - which roll inside.
For other sticklengths these curves are called epitrochoids resp. hypotrochoids.
Epi and Hypocycloids 001
Circle rolling inside a bigger circle, tracing out a rose curve. The random dots help to show the rotating plane centered on the contact point of 2 rolling curves. The significance is that the contact point to the tracing point is the normal of the curve, and this is true for any curve rolling on another curve.

Epi-_and_Hypocycloids.pdf