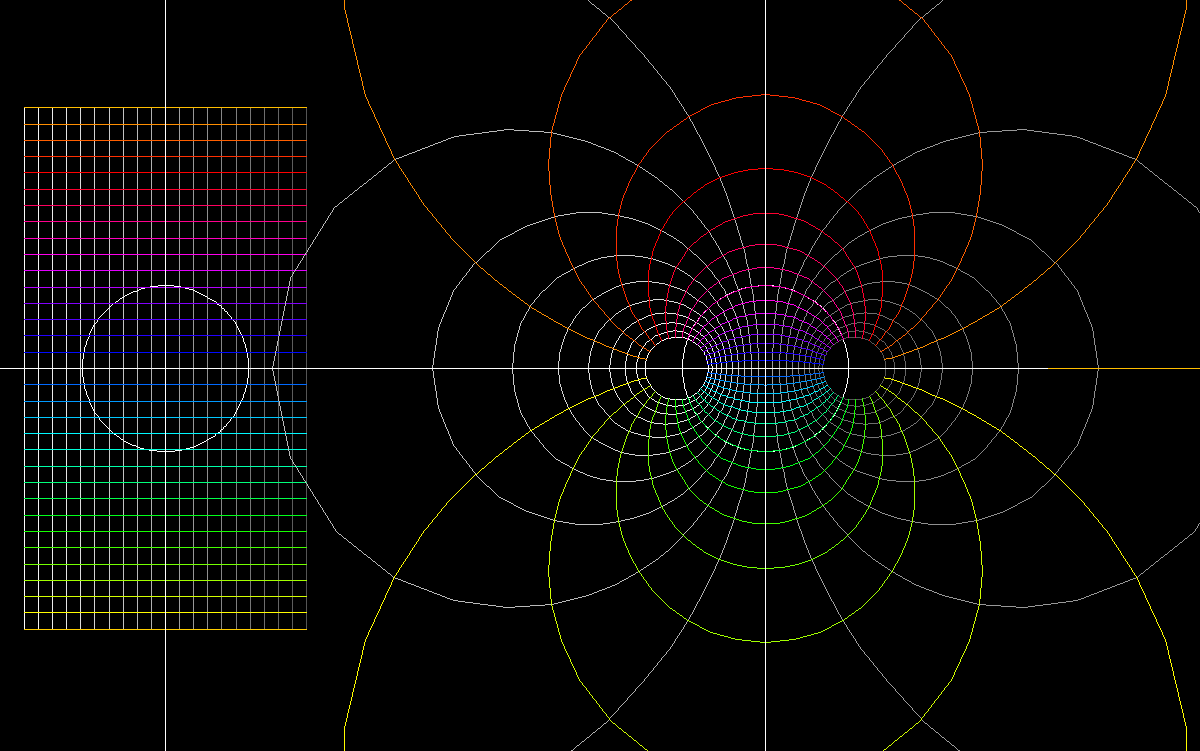
z → tanh(z/2) = sinh(z/2)/cosh(z/2) = (exp(z) - 1)/(exp(z) + 1)domain:
-1.7 ≦ Re(z) ≦ 1.7, -pi ≦ Im(z) ≦ pi.Since
i*tan(z) = tanh(i*z), one can use this image to visualize the complex tangent function, just rotate the image through 90 degrees.

z → tanh(z/2) = sinh(z/2)/cosh(z/2) = (exp(z) - 1)/(exp(z) + 1)-1.7 ≦ Re(z) ≦ 1.7, -pi ≦ Im(z) ≦ pi.i*tan(z) = tanh(i*z), one can use this image to visualize the complex tangent function, just rotate the image through 90 degrees.
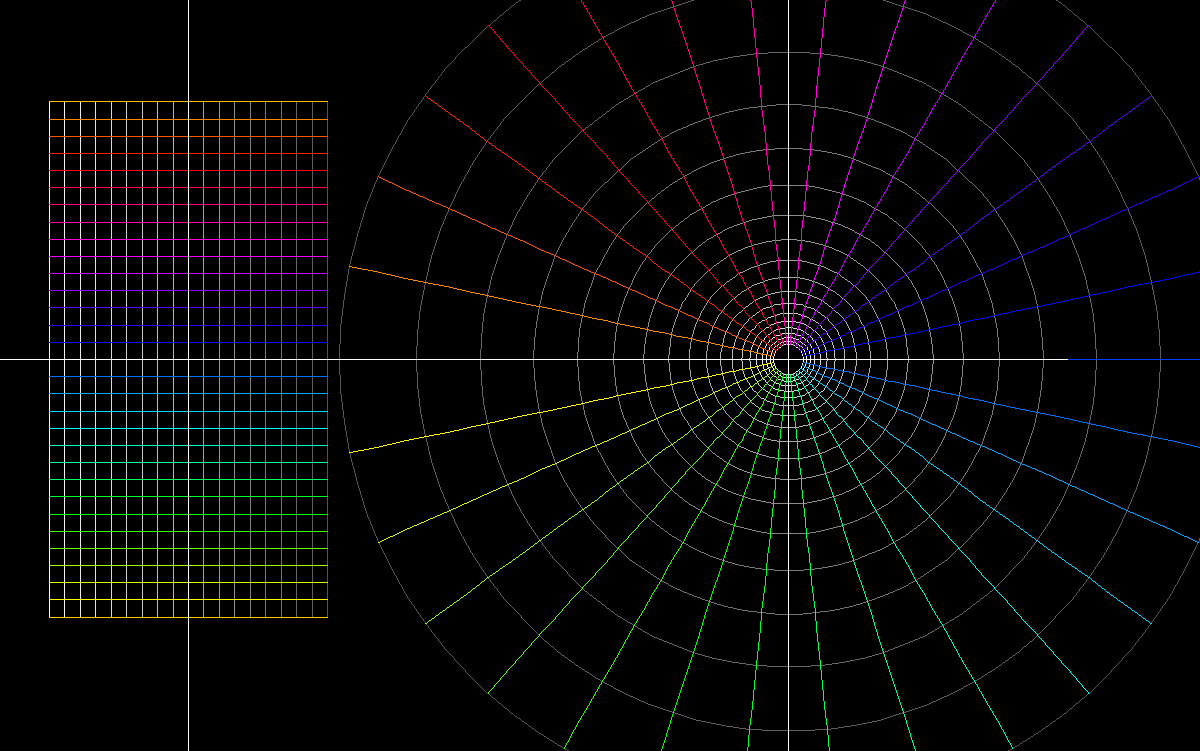
z → w = exp(z) → (w - 1)/(w + 1).
This is the 1st step, the exponential map from the cartesian grid to the conformal polar grid.
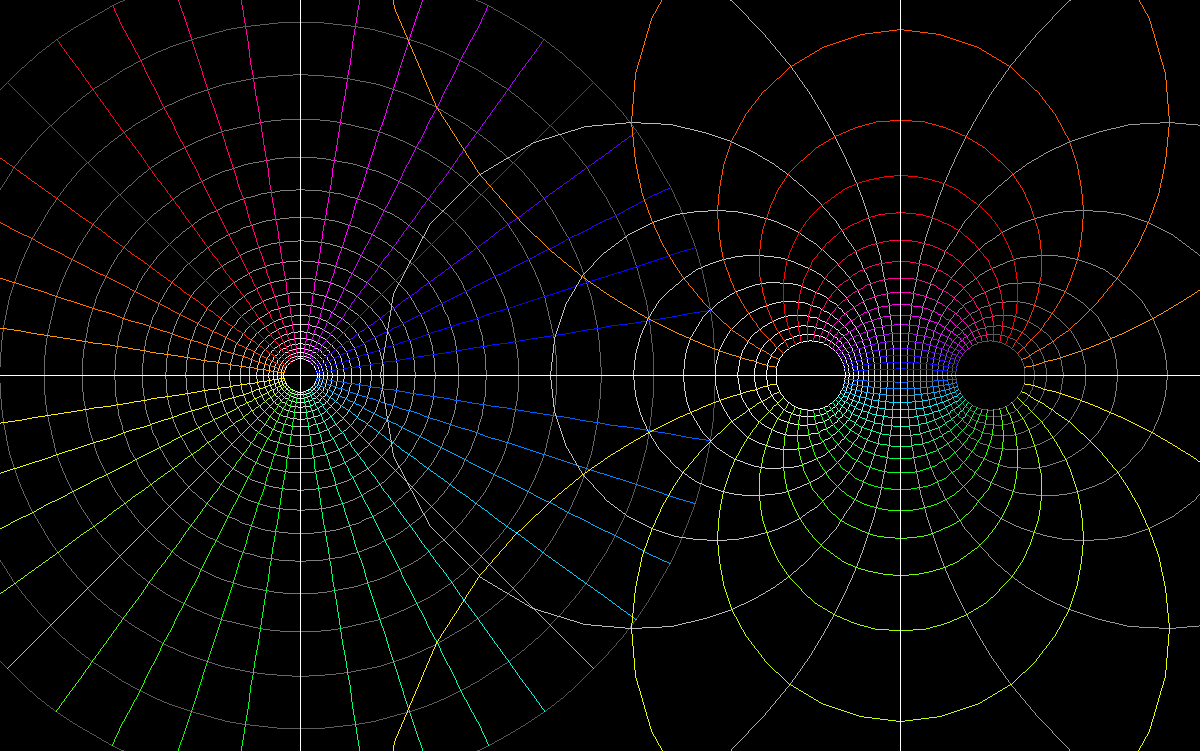
w → (w - 1)/(w + 1), from the polar grid to the tanh-image,