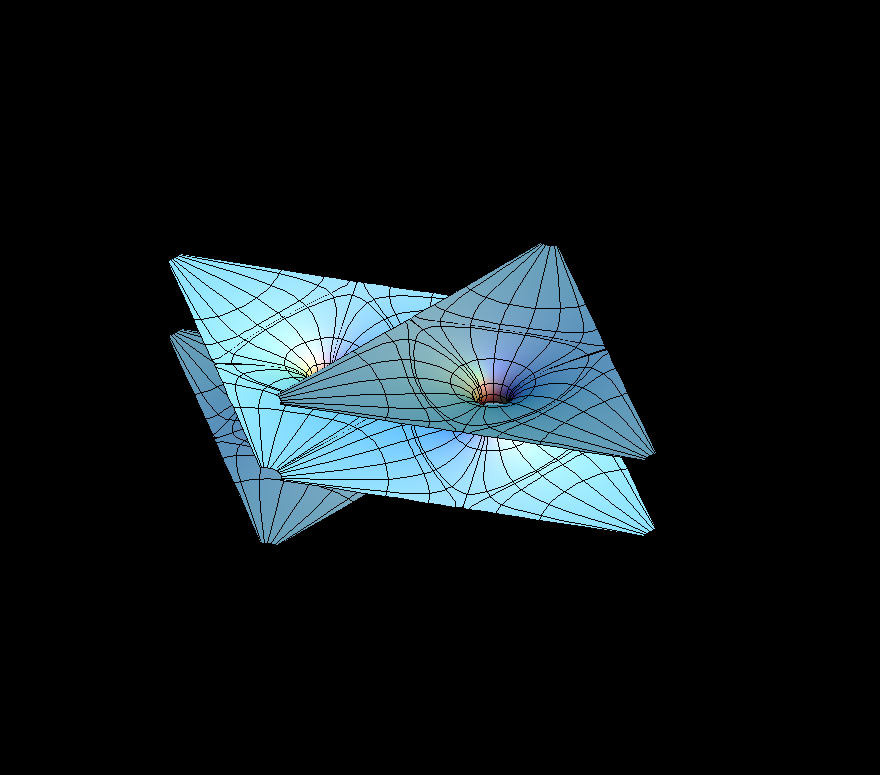

This surface is built from pieces which one can call “triangular catenoids”: Instead of circle boundaries these pieces have equilateral triangles as boundary. One can numerically compute the triangular catenoids from their boundary triangles.
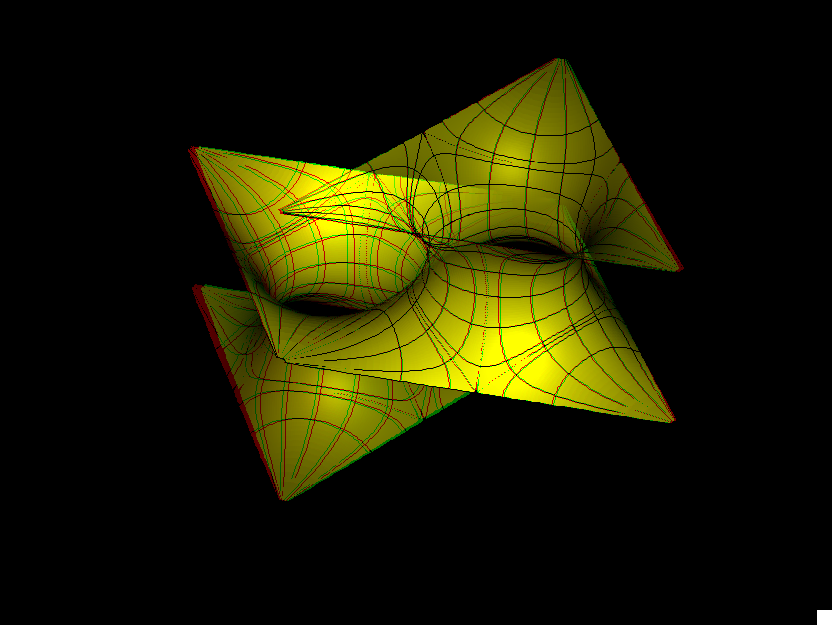
This is a 1-parameter family of triply periodic surfaces. The surfaces are made of pieces which one could call “triangular catenoids”; annular Plateau solutions bounded by two parallel equilateral triangles. In the morphing aa changes the height-to-edge length ratio of these triangular catenoids. Observe that, as in the case of circles bounding catenoids, the distance between the triangles has to be small enough and then they bound a stable and an unstable triangular catenoid. In the PD-family with dd=0 one can observe analogous “square catenoids”, except that our parametrization does not emphasize them.
When Alan Schoen found more triply periodic surfaces around 1970 he named these “Schwarz's H surfaces”. (Maybe Schwarz constructed only one member of the family.) Later, the Swedish chemist, Lidin, found another embedded example in the associate family when aa is approximately 0.55, and the associate family parameter is 0.7139, which is about 64.25 degrees.
For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see either [KWH], or pages 192--217 of [DHKW].