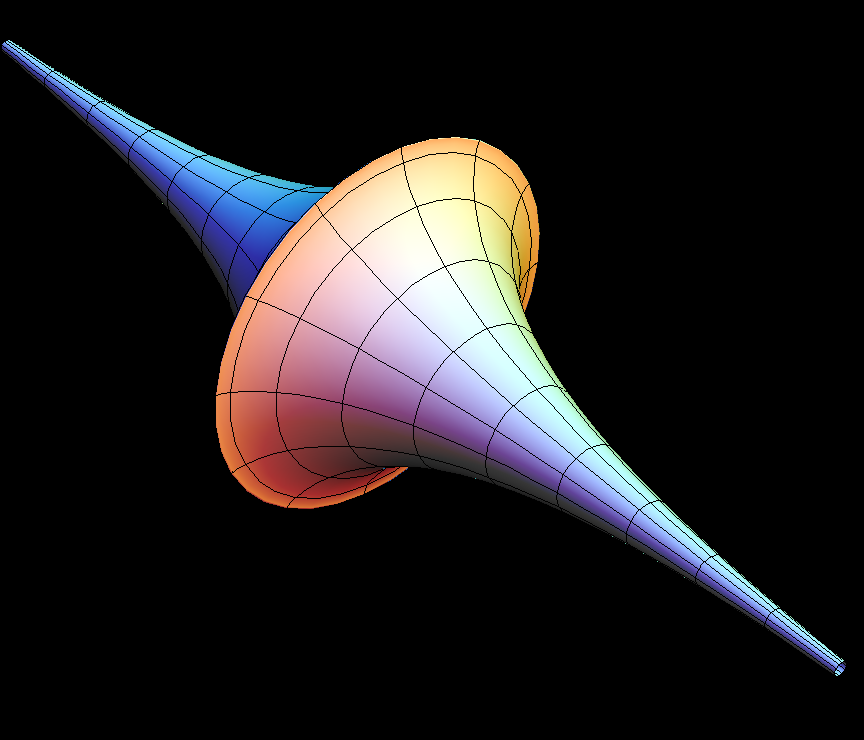
Pseudosphere
Hermann Karcher
The Pseudosphere is a surface of revolution (of the Tractrix)
and has Gaussian curvature minus one, or in other words, the
product of its principal curvatures is -1. On a surface of
revolution, this translates into a simple analytic property:
Parametrize the meridian curve by arc length s ---> (r(s) , h(s)),
r'^2 + h'^2 = 1. Then r is a solution of the differential equation
r'' = r, and consequently h is also known---it is the anti-derivative
of sqrt(1 - (r')^2).
The Pseudosphere is best known because its intrinsic geometry is
hyperbolic, the meridians are a family of asymptotic geodesics
and the orthogonal latitudes are therefore a geodesically parallel
family of "horocycles", i.e. limits of circles as their midpoints
converge to the limit point of the asymptotic geodesics.
This Pseudosphere is obtained by the construction which relates
solutions of the Sine-Gordon equation to surfaces of Gaussian
curvature -1, here the solution is a one-soliton solution:
q(u,v) := 4 arctan(exp(u)).
The parametrization obtained has another remarkable property: The
diagonal curves in ALL the parameter quadrilaterals have the
same length! Nets used for fishing also have such equiquadrilaterals
as meshes; the mathematical term is "Tchebycheff net". Such
Tchebycheff nets exist on all surfaces which are isometric immersions
of (portions of) the hyperbolic plane. This fact plays a key role in the
proof of Hilbert's theorem which says: There is no smooth isometric
immersion of the whole hyperbolic plane into euclidean threespace.
See also the "Tractrix" under Planar Curves.