Chen Gackstatter Minimal Surface

About the Chen-Gackstatter Minimal Surface and its Analogs with Higher Dihedral Symmetry

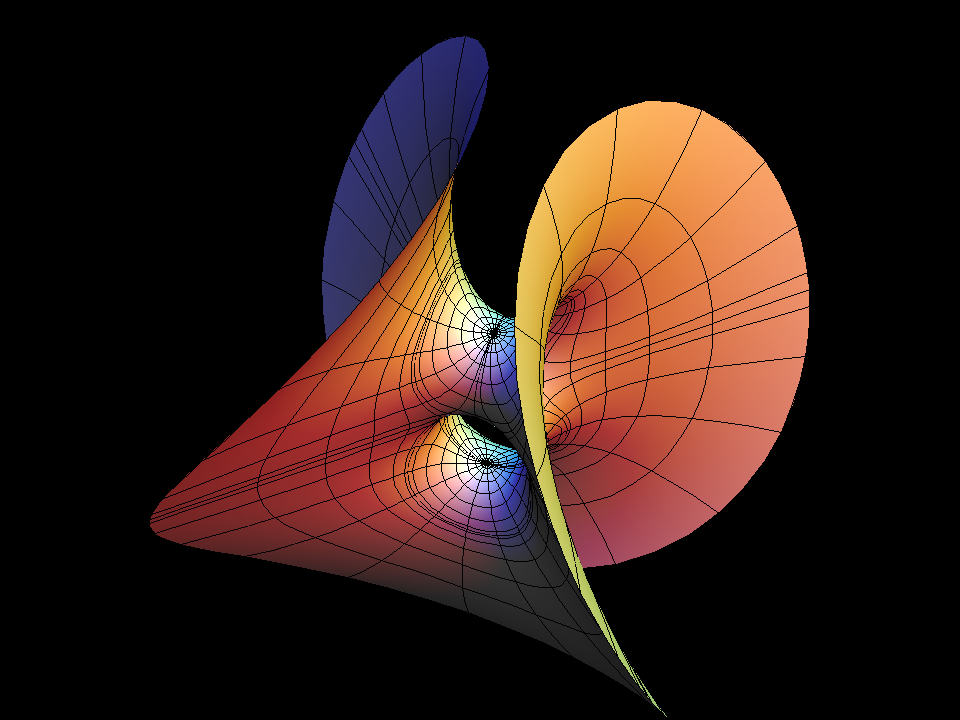
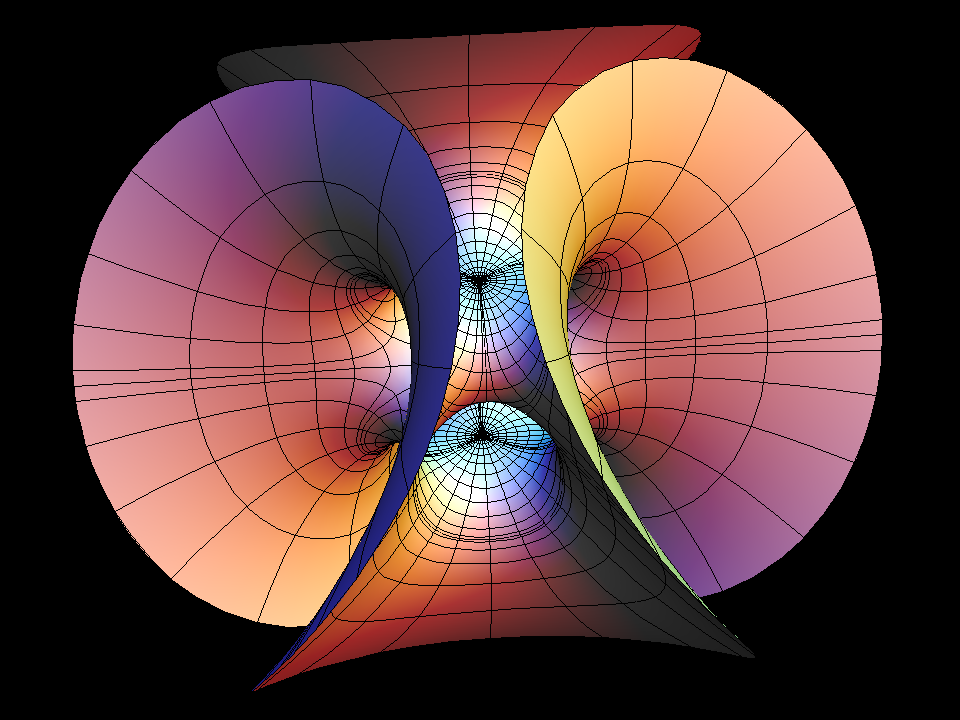
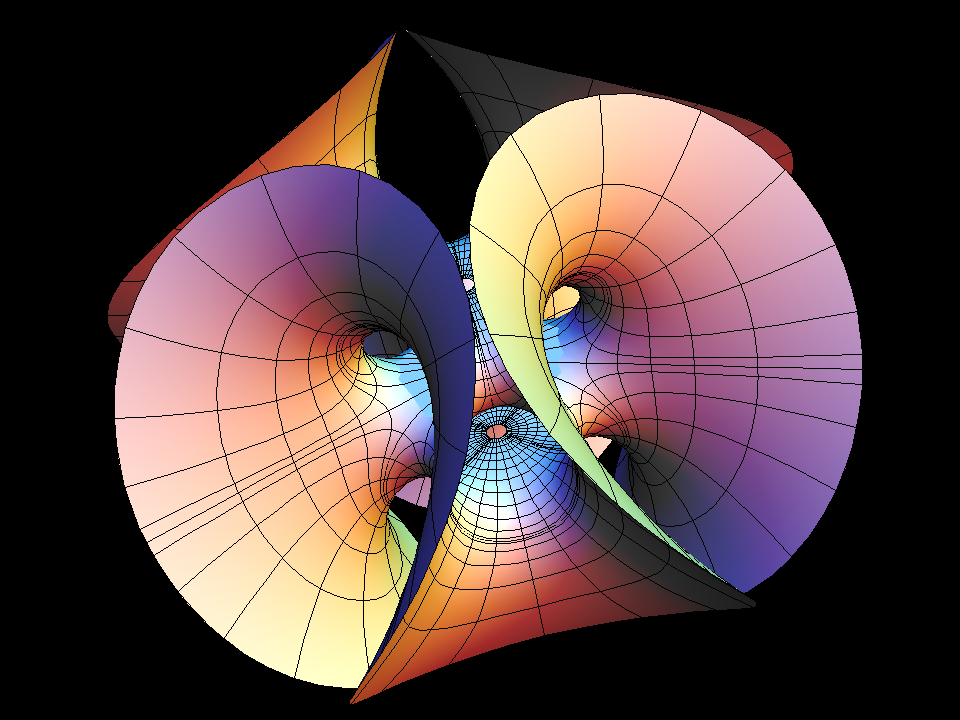
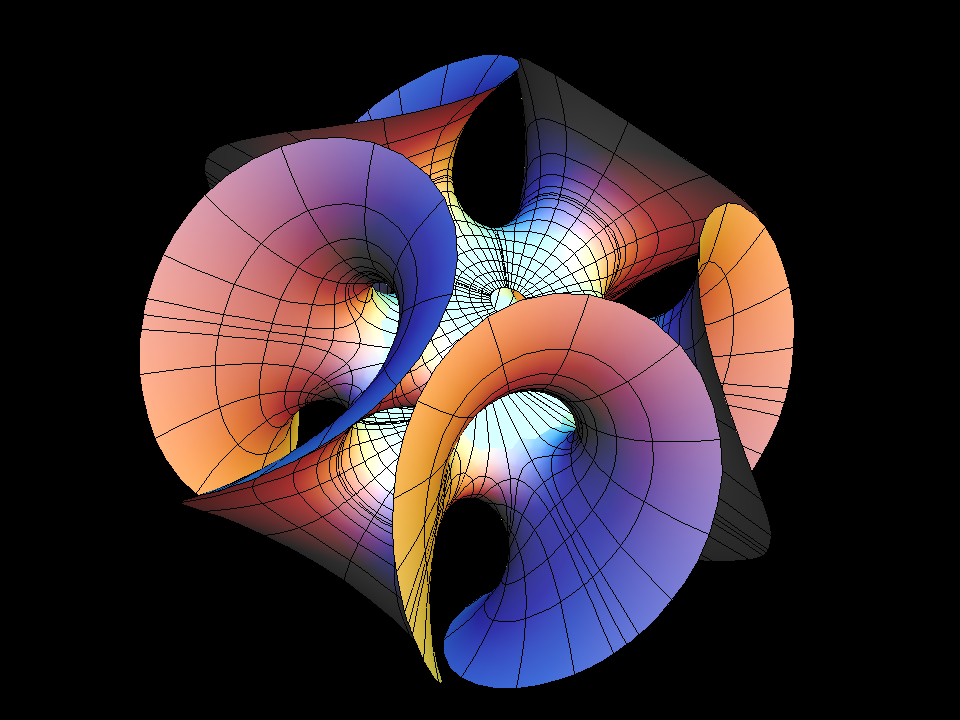
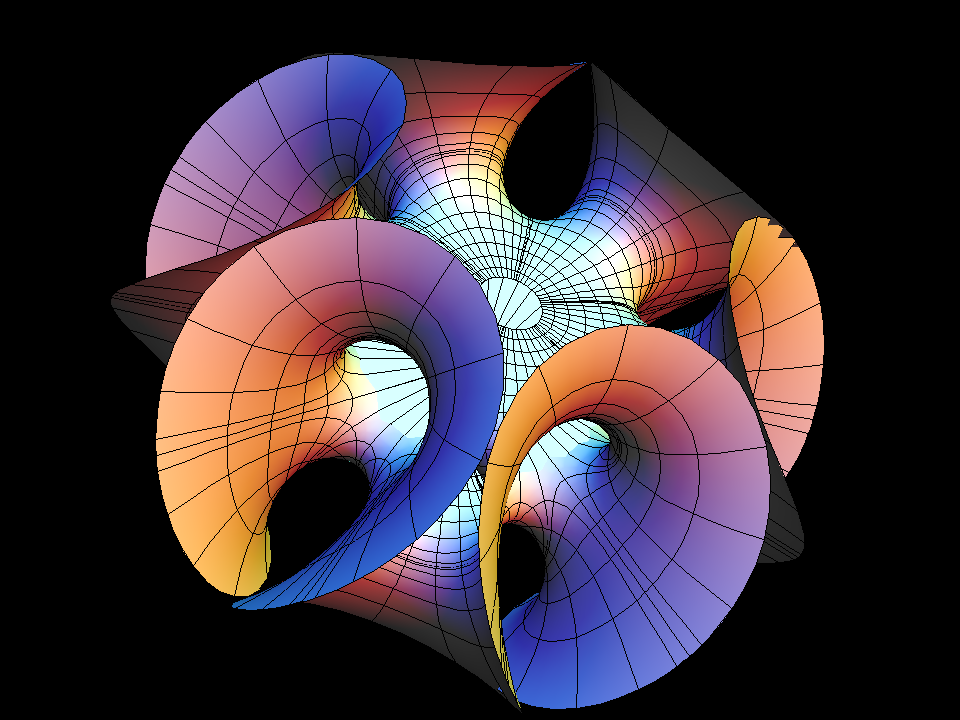
This surface is the first finite total curvature immersion of a Riemann surface of genus ≻ 0 (here the square Torus).

It looks like an Enneper Surface with a handle added parallel to its center saddle. This description determines the Gauss map only up to a multiplicative constant (cc), which we took as the morphing parameter. If this parameter is general then we get a doubly periodic minimal immersion of the plane. The morphing indicates how the period can be closed for one value of cc with the intermediate value theorem. The resemblance with the standard Enneper Surface is emphasized by using polar coordinates around the puncture. The dd=3 surface is an analogue which can be viewed as a higher order (120 degree symmetric) Enneper Surface with a Y-shaped handle glued in. It was first published in a 1988 Vieweg Calendar by Polthier and Wohlgemuth....

Formulas are from:

• [K2] Construction of Minimal Surfaces, H Karcher , in “Surveys in Geometry”, Univ. of Tokyo, 1989, and Lecture Notes No. 12, SFB 256, Bonn, 1989, pp. 1 — 96.

For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see:

• [KWH] H. Karcher, F. Wei, and D. Hoffman, The genus one helicoid, and the minimal surfaces that led to its discovery, in “Global Analysis in Modern Mathematics, A Symposium in Honor of Richard Palais' Sixtieth Birthday”, K. Uhlenbeck Editor, Publish or Perish Press, 1993
• [DHKW] U. Dierkes, S. Hildebrand, A. Kuster, and O. Wohlrab, Minimal Surfaces I, Grundlehren der math. Wiss. v. 295 Springer-Verlag, 1991