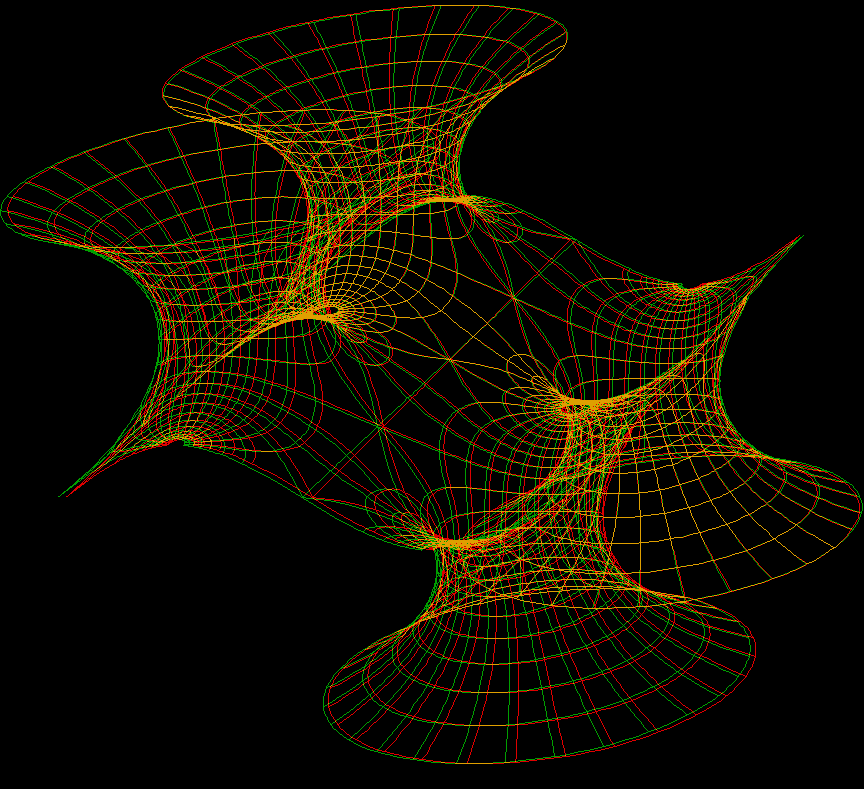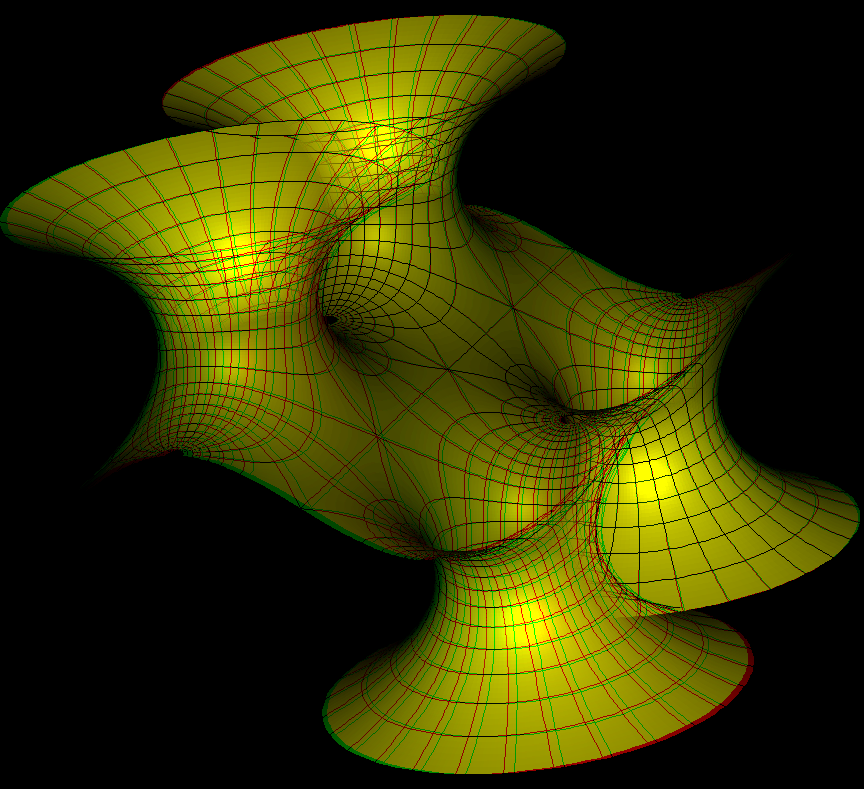

Why do mathematicians say: “This minimal surface is parametrized by a twice punctured torus”?
The half-Catenoids represent punctures. Why “two punctures”? The left and the right boundary of the shown surface are straight lines and in the middle between them is a third line. Straight lines on a minimal surface imply 180 degree rotation symmetries around these lines - clearly visible. These rotation symmetries imply that translation of the left line to the right line is a translation symmetry of the surface: The surface is periodic in this direction and we now know the corresponding period translation.
The surface is also reflection symmetric with respect to planes orthogonal to the above lines. Three such planes pass through the centers of neighboring polar center “holes” and two such planes each split in half one of the up half-catenoids and its neigboring down half-catenoid. Reflections in two such planes create a translation symmetry orthogonal to the one which we already know. The shortest of them goes from the front edge to the middle - another “period translation”.
The front half of the shown surface piece is therefore a “fundamental domain” for the translational symmetries of a “doubly periodic” minimal surface. If we “identify corresponding points of the boundary of the fundamental domain” with the help of the above period translations, then we get an abstract rectangular torus with two half-catenoid punctures! — The Gauss map of this surface is g(z) = c*Je(z), where Je is a Jacobi type elliptic function with two simple poles and two simple zeros, on an arbitrary rectangular torus.
And why are there the “polar center holes”?
For this surface we have chosen the same kind of parameter lines as for the catenoid, namely the inverse image of a polar grid on the Riemann sphere under the Gauss map of the surface. In other words: the Gauss map of this surface sends the chosen parameter lines to the longitude and latitude circles of the Riemann sphere! But why the holes? Since complex differentiability is essential for minimal surfaces we prefer to use infinitesimally square grids - see the complex exponential function. These conformal polar grids are symmetric with respect to the unit circles and neither the inside nor the outside of the unit circle can be covered with finitely many “infinitesimally square” parameter rectangles.
And why are there vertices in the parameter grid on the surface where four parameter lines cross instead of the normal crossing of two? These are points where the derivative of the Gauss map has a simple zero, like the squaring function at zero. The Gaus map of the surface sends a small half disk around such a point to a full disk around the image on the Riemann sphere. — Moreover, this surface has point reflection symmetries with respect to these points.
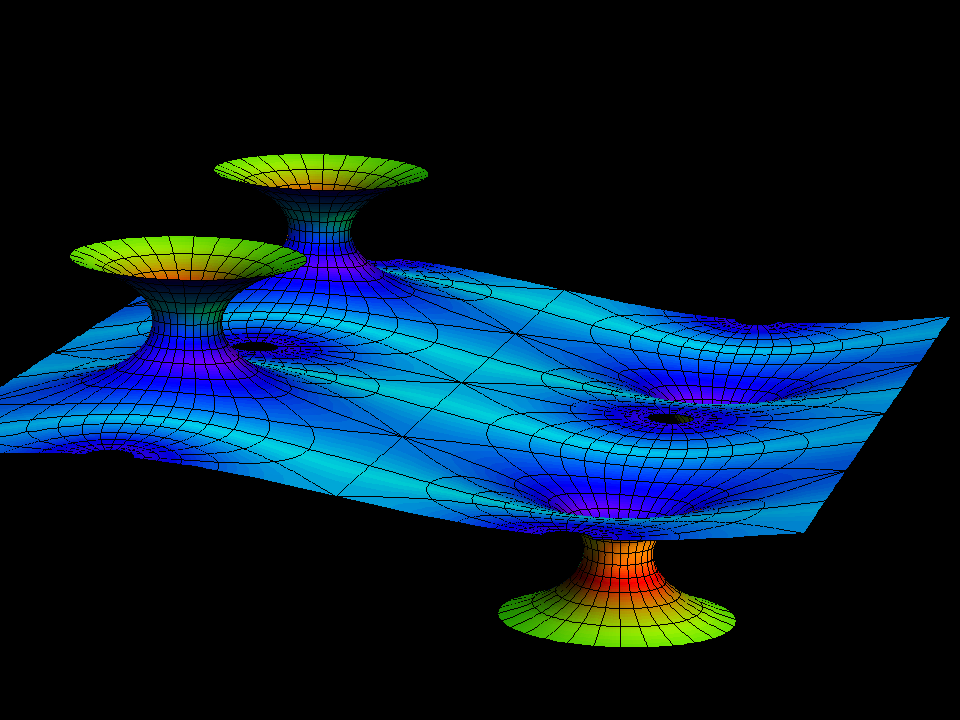
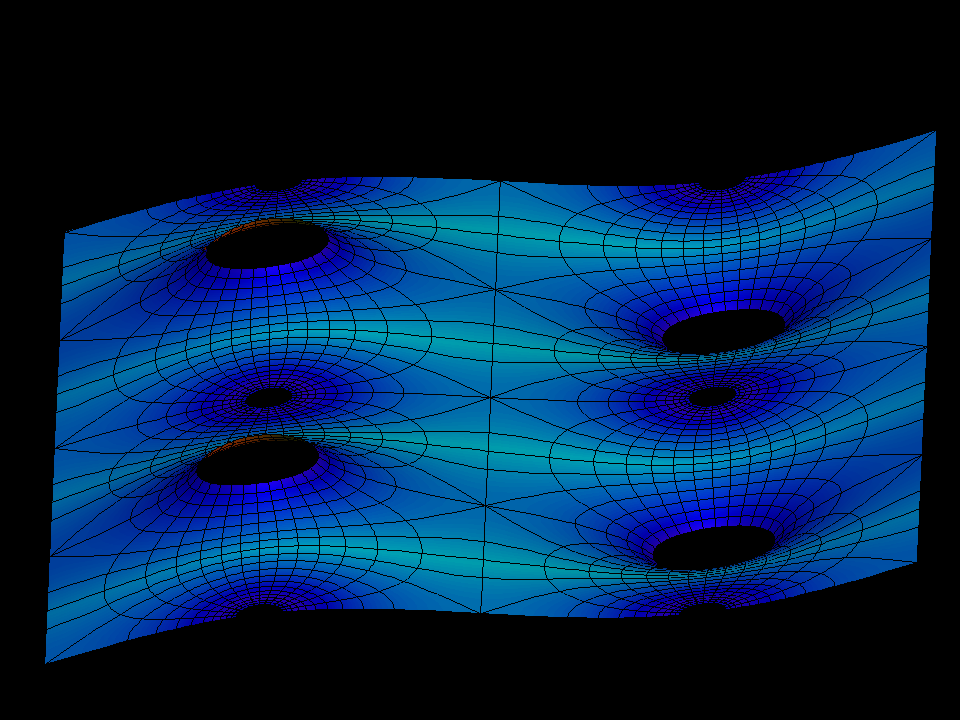
This animation shows how the parameter c of the gauss map g(z) = c*Je(z) changes the
geometry of the surface. The surface normal 「n(p)」 at the point p where the symmetry curve
from one up half-catenoid to its neighboring down half-caenoid crosses the straight
symmetry line is determined by c. (These are the points where the Gaus map has
derivative zero.)
The surfaces in this animation are scaled so that the distance between the bounding straight symmetry lines is always the same. A large number c makes the half-catenoids skinny a small number makes them fat.