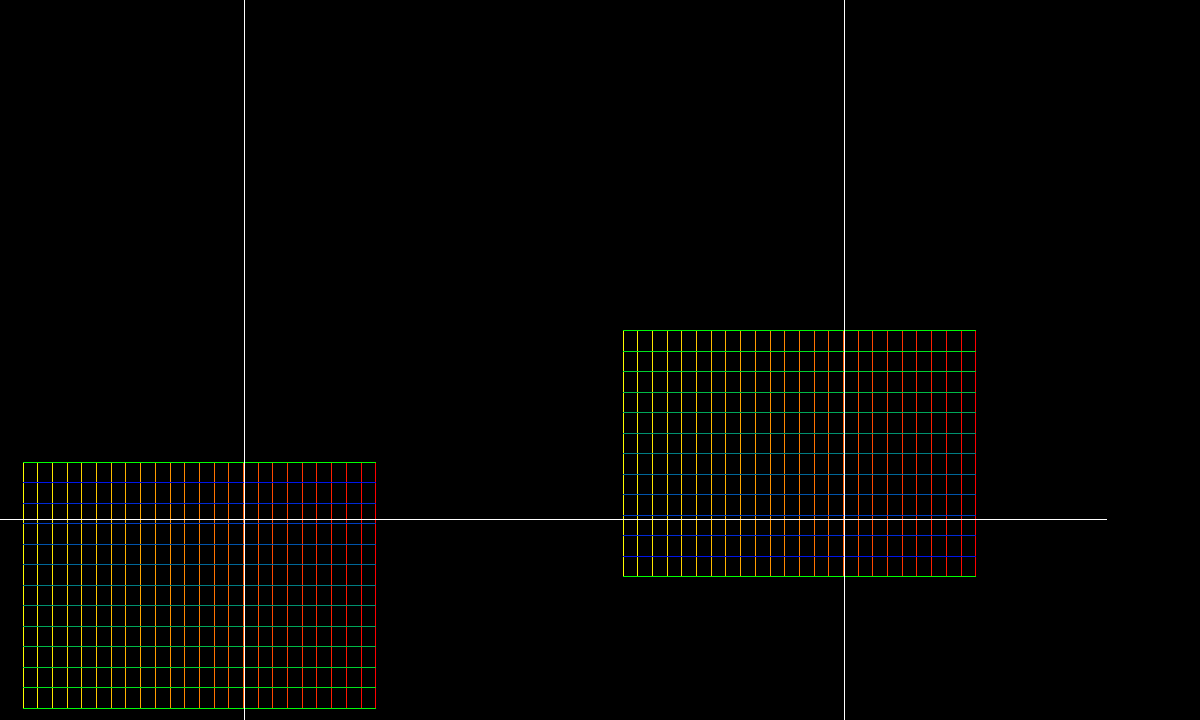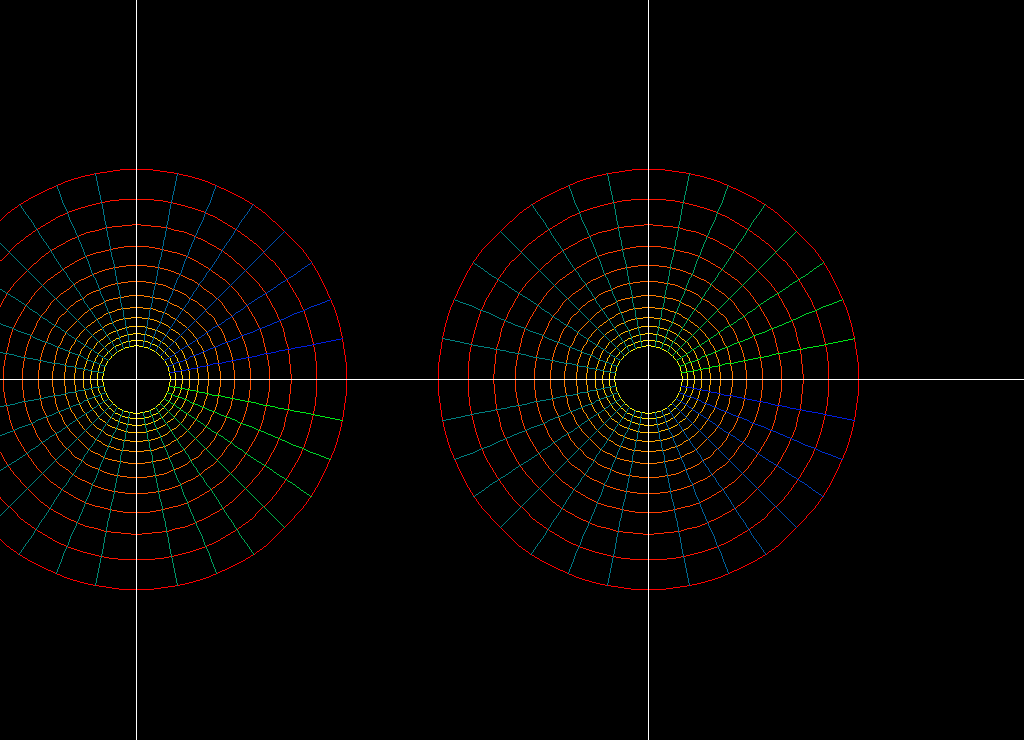
conj(z) + c*z^2domain: conformal polar grid,
0.4 ≦ |z| ≦ 2.5, 0 ≦ angle ≦ 2*pimorph :
0 ≦ c ≦ 0.4The image shows in several ways that the map is not conformal. Most obvious is the development of fold lines - conformal maps never have them. Looking at smaller details we see that the “curved squares” of the domain are mapped to parallelograms - this contradicts the definition of conformality. Another proof of not being conformal are the outward pointing deltoid-cusps - conformal maps only develop inward pointing cusps, compare Polynomial Example