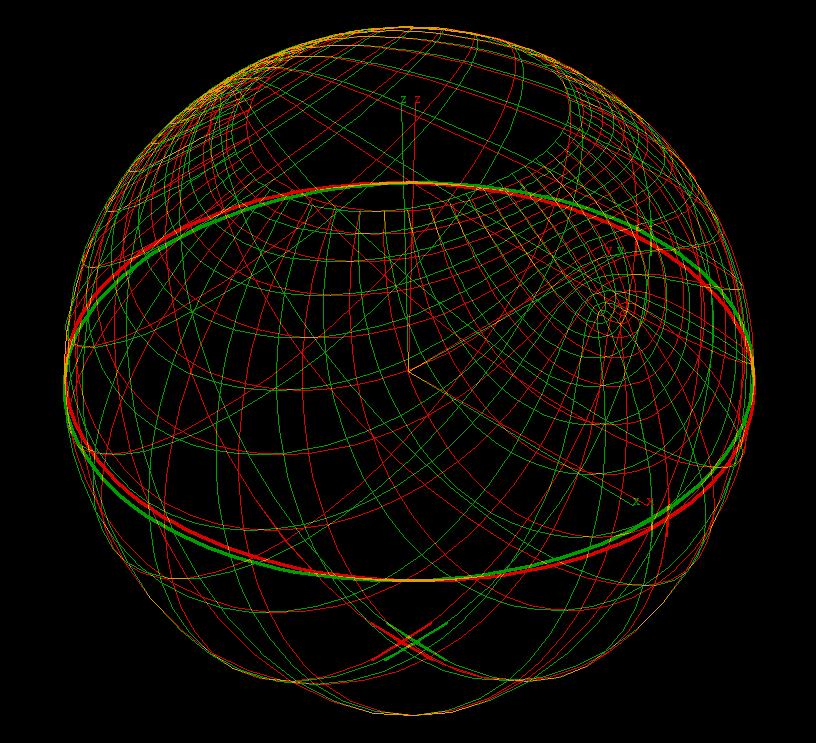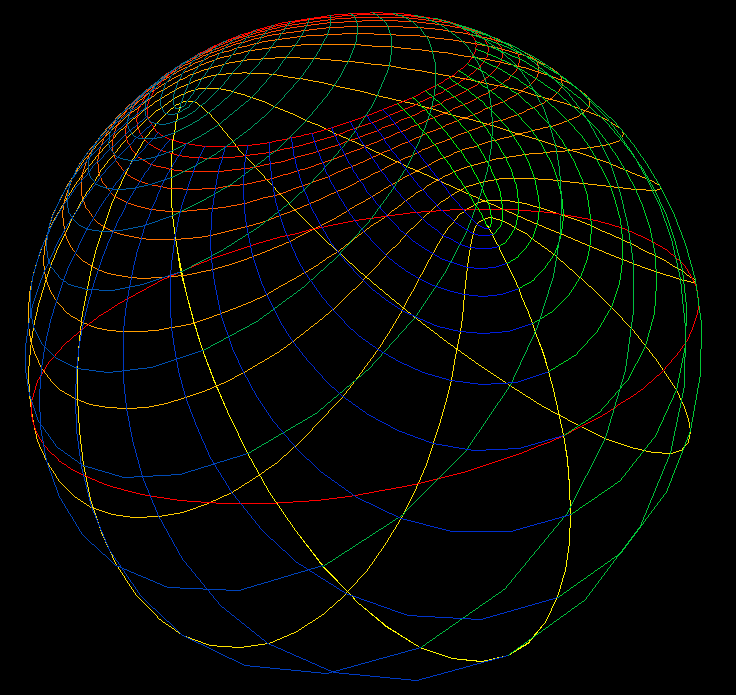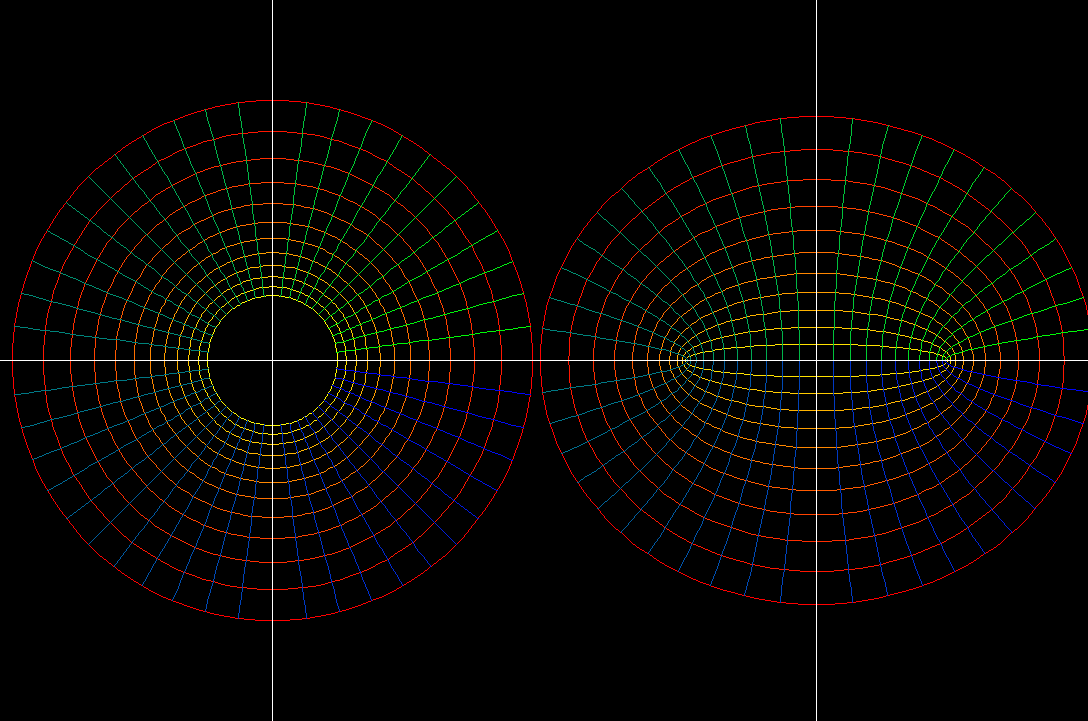
z ⟶ f(z) = z + 1/z, domain: a ≺ |z| ≺ 4, morph: 1 ≺ a ≺ 2.The radial parameter lines
r ⟶ r*exp(i*t)
, t = constant, are mapped to
Hyperbolas
r ⟶ r*exp(i*t) + 1/r*exp(-i*t) = (r+1/r)*2cos(t) + i*(r-1/r)*2sin(t)The angular parameter lines
t ⟶ r*exp(i*t), r = constant, are mapped to
Ellipses
t ⟶ r*exp(i*t) + 1/r*exp(-i*t) = 2(r+1/r)*cos(t) + i*2(r-1/r)*sin(t)All these ellipses and hyperbolas have the same focal points, therefore they are called “confocal”.